Annu. Rev. Astron. Astrophys. 1994. 32: 531-590 Copyright © 1994 by Annual Reviews. All rights reserved

3.1. Cosmological Nucleosynthesis

The main argument for nonbaryonic dark matter is associated with Big Bang nucleosynthesis. This is because the success of the standard picture in explaining the primordial light element abundances [X(⁴He) 0.24, X(²D) ~ X(³He) ~ 10^-5, X(⁷Li) ~ 10^-10] only applies if the baryon density parameter _b is strongly constrained. Walker et al (1991) find that it must lie in the range

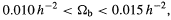
(3.1)

where the upper and lower limits come from the upper bounds on ⁴He and ²D + ³He, respectively. The upper limit implies that _b is well below 1, which suggests that no baryonic candidate could provide the critical density required in the inflationay scenario. The standard scenario therefore assumes that the total density parameter is 1, with only the fraction given by (3.1) being baryonic. Until recently, cold inos seemed to be most compatible with large-scale structure observations; this led to the popularity of the CDM scenario.

Recently, X-ray data on the mass of gas in groups and clusters of galaxies suggest that the standard CDM picture may not be satisfactory. Although the gas does not suffice to explain all the dark matter, the ratio of the visible baryon mass (i.e. the mass in the form of stars and hot gas) to total mass is still anomalously high compared to the mean cosmic ratio implied by Equation (3.1). For example, the baryon fraction is 13% for the small group HCG62 (Ponman & Bertram 1993) and it tends to be in the range 20-30% for rich clusters. In particular, ROSAT observations of Coma suggest that the baryon fraction within the central 3 Mpc is about 25%, which is five times as large as the standard cosmological ratio (White et al 1993). It is hard to understand how the extra baryon concentration would come about since dissipation should be unimportant on these scales and most other astrophysical processes (such as winds and supernovae) should decrease the local baryon fraction. [See, however, Babul & Katz (1993) for a contrary view.] Unless one invokes a cosmological constant, this suggests that either the cosmological density is well below the critical value or the baryon density is much higher than implied by the standard cosmological nucleosynthesis scenario.

In the past few years considerable work has focused on the question of whether one can circumvent condition (3.1) by invoking a first-order phase transition at the quark-hadron era. The idea is that the transition would generate fluctuations in the baryon density. Neutrons would then diffuse from the overdense regions (because their cross-section is less than that of the protons), which would lead to variations in the neutron-to-proton ratio. One can then produce deuterium in the regions where the density is low, without appreciably modifying the average helium production (Applegate et al 1987, Alcock et al 1987). However, there is still a problem getting the observed lithium abundance. This arises because, as one varies _b, X(⁷Li) has a minimum at around _b ~ 0.01, and the observed abundance almost exactly matches this minimum. Any fluctuations in the baryon density will therefore tend to lead to an overabundance of lithium.

Interest in the effects of the quark-hadron transition was revived by the suggestion of Malaney & Fowler (1988) that neutrons could diffuse back into the overdense regions and destroy lithium, provided that the separation between the nucleation sites was finely-tuned (d ~ 10 m). However, in this case, helium may be overproduced. A detailed numerical investigation of the effects of simultaneously varying _b, d, the amplitude of the baryon density fluctuations (R), and the volume fraction at high density (f_v) by Kurki-Suonio et al (1990) suggested that, although values of R as large as 100 are compatible with observation if d < 300 m, one can never have _b = 1. More recently, Mathews et al (1993) have argued that the largest possible value for the baryon density is _b = 0.09h^-2, so a critical density of baryons still seems to be excluded unless H₀ < 35. For an up-to-date review of inhomogeneous nucleosynthesis, see Malaney & Mathews (1993).