Annu. Rev. Astron. Astrophys. 1994. 32: 531-590 Copyright © 1994 by Annual Reviews. All rights reserved

5.2. Enrichment Constraints

One of the strongest constraints on the spectrum of Population III stars comes from the fact that stars in the mass range 4 M to M_c 200 M should produce an appreciable heavy element yield (Arnett 1978), either via winds in their main-sequence phase or during their final supernova phase. We take the yield Z_ej to be 0.01 for 8 M < M < 15 M, 0.5-(M/6 M)^-1 for 15 M < M < 100 M, and 0.5 for 100 M < M < M_c (Wheeler et al 1989). Carr et al (1984) took z_ej = 0.2 for 4 M < M < 8 M on the assumption that such stars explode as a result of degenerate carbon burning. However, it seems possible that they evolve to white dwarfs without exploding, so Figure 2 assumes there is no enrichment for M < 8 M. Whether Population III stars are pregalactic or protogalactic, the enrichment they produce cannot exceed the lowest metallicity observed in Population I stars (Z = 10^-3). One infers that the density of the stars must satisfy

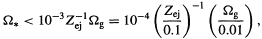
(5.1)

where _g is the gas density before the stars form, assumed to be around 0.01 in view of the Equation (3.1). This enrichment constraint is shown in Figure 2 (note that it is stronger than indicated by Carr et al (1984) because they assumed _g = 0.1.] It immediately excludes neutron stars or ordinary stellar black holes from explaining any of the dark matter problems unless the Population III precursors are clumped into clusters whose gravitational potential is so high that ejected heavy elements cannot escape (Salpeter & Wasserman 1993). If one wants to produce the dark matter without contravening the enrichment constraint, the most straightforward solution is to assume that the spectrum either starts above M_c (as in the black hole scenario) or ends below 8 M (as in the brown dwarf or white dwarf scenario), so that there is no pregalactic enrichment at all.