Annu. Rev. Astron. Astrophys. 1994. 32: 531-590 Copyright © 1994 by Annual Reviews. All rights reserved

7.1. Macrolensing Constraints on Compact Objects

If one has a population of compact objects with mass M and density parameter _c, then the probability P of one of them image-doubling a source at redshift z 1 and the separation between the images are given by

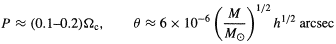
(7.1)

(Press & Gunn 1973). One can therefore use upper limits on the frequency of macrolensing for different image separations to constrain _c as a function of M. Although optical searches, VLA, and the Hubble Space Telescope (HST) can only constrain objects down to 10¹⁰ M (corresponding to a resolution of 0.1 arcsec), speckle cameras (with a resolution of 10^-2 arcsec) can get down to 10⁸ M, while VLBI and VLBA (with resolutions of 1 and 0.1 milliarcsec) can search for objects as small as 10⁶ M and 10⁴ M. The best strategy is to look for dim images near bright objects (Nemiroff & Bistolas 1990), which requires a large dynamic range, but one can also look for circular distortions and gravity rings (Saslaw et al 1985, Turner et al 1990). The usual approach is to derive the "detection volume," defined as the volume between the source and observer within which the lens would need to lie in order to produce an observable effect (Nemiroff 1989, Kassiola et al 1991). Limits are then obtained by adding the detection volume for each source and comparing this to the volume per source expected for a given _C.

There have been several optical and radio surveys to search for multiply-imaged quasars (Hewitt et al 1989, Bahcall et al 1992b). In particular, Hewitt (1986) used VLA observations to infer _C(10¹¹-10¹³ M) < 0.4, Nemiroff (1991b) used optical QSO data from Crampton et al (1989) to infer _C(M > 10^9.9 M) < 1 and _C(M > 10^10.3 M) < 0.25, and Surdej et al (1993) used data on 469 highly luminous quasars (including HST observations) to infer _C(10¹⁰-10¹² M) < 0.02. To probe smaller scales, one must use high resolution radio sources: Kassiola et al (1991) have used lack of lensing in 40 VLBI objects to infer _C(10⁷-10⁹ M) < 0.4, while a study by Patnaik et al (1992) of 200 flat spectrum radio sources may lead to a limit _C(10⁶-10⁹ M) < 0.01 (Henstock et al 1993). (Flat spectrum sources are dominated by a single core and are therefore more likely to be lensed: this limit assumes that no sources are identified and is not included in Figure 5.)

Future observations could strengthen these constraints considerably: Speckle interferometry could push _C(10⁸-10¹⁰ M) down to 0.01, while VLBA could push _C(10⁵-10⁸ M) down to 0.001 (Surdej et al 1993). These two limits are shown as broken lines in Figure 5. Another interesting possibility is to search for lensing distortions in radio jets (Kronberg et al 1991): this would permit the detection of objects with mass around 10⁶ M since the Einstein radius for such objects is of order milliarcsecs and therefore comparable to the characteristic jet scale. Of course, jets may be intrinsically kinky but Wambsganss & Paczynski (1992) have pointed out that this poses no problem if one uses VLBI and VLBA maps of the jets in image-doubled quasars because only one of the images would then be kinked. Their numerical simulations show that the effects of supermassive black holes would be numerous and obvious. Lenses between 0.3 and 3 × 10⁶ M would certainly be noticeable for a dynamic range of 100:1 and may have already been excluded (Heflin et al 1991, Garrett et al 1994).