Copyright © 1994 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1994. 32:
531-590 Copyright © 1994 by Annual Reviews. All rights reserved |
8.2. Infrared Background from VMOs
We now compare these limits with the background expected from a population
of VMOs. This can be predicted very precisely since all VMOs have a surface
temperature Ts of about 105 K and generate
radiation with efficiency

 0.004.
We normalize the VMO density parameter to the value
0.004.
We normalize the VMO density parameter to the value
 *
*
 0.1 required to
explain galactic halos and assume that they produce black-body radiation
with
temperature Ts. If the radiation is affected only by
cosmological redshift, its
density and peak wavelength at the present epoch should be
0.1 required to
explain galactic halos and assume that they produce black-body radiation
with
temperature Ts. If the radiation is affected only by
cosmological redshift, its
density and peak wavelength at the present epoch should be
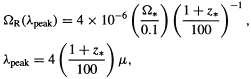
| (8.1) |
where z* is the redshift at which the VMOs
burn. We can place an upper limit
on z* by noting that the main-sequence time
of a VMO is tMS
 2 × 106y
(independent of mass), so that z* cannot
exceed the redshift when the age of
the Universe is tMS. This implies
z* < 240h-2/3 and so
2 × 106y
(independent of mass), so that z* cannot
exceed the redshift when the age of
the Universe is tMS. This implies
z* < 240h-2/3 and so
 peak <
15 µ and
peak <
15 µ and
 R
> 10-6 for h > 0.5. We can place a lower limit
on z* from UV/optical
background light limits. As discussed by
McDowell (1986)
and Negroponte (1986),
these imply a constraint on the density of VMOs burning at any redshift
z*. If one requires
R
> 10-6 for h > 0.5. We can place a lower limit
on z* from UV/optical
background light limits. As discussed by
McDowell (1986)
and Negroponte (1986),
these imply a constraint on the density of VMOs burning at any redshift
z*. If one requires  *
*
 0.1, this places a
lower limit on z*, mainly because one
needs the radiation to be redshifted into the near-IR band, where the
background
light limits arc weaker. In the absence of neutral hydrogen absorption, one
requires z* > 30, which implies
0.1, this places a
lower limit on z*, mainly because one
needs the radiation to be redshifted into the near-IR band, where the
background
light limits arc weaker. In the absence of neutral hydrogen absorption, one
requires z* > 30, which implies
 peak > 1
µ and
peak > 1
µ and
 R <
10-5. The peak of the
VMO background must then lie somewhere on the heavy line in
Figure 6 and
the spectrum must lie within the region bounded by the broken line. Note
that
the observational limits are only just beginning to constrain the VMO
scenario
and they may never be able to exclude it if
z* is so large (> 200) that most of the
VMO light is pushed beyond 10 µ, where it would be hidden by
interstellar dust.
R <
10-5. The peak of the
VMO background must then lie somewhere on the heavy line in
Figure 6 and
the spectrum must lie within the region bounded by the broken line. Note
that
the observational limits are only just beginning to constrain the VMO
scenario
and they may never be able to exclude it if
z* is so large (> 200) that most of the
VMO light is pushed beyond 10 µ, where it would be hidden by
interstellar dust.
The constraints on the VMO scenario would be much stronger if the light
was reprocessed by dust as discussed by many workers
(McDowell 1986,
Negroponte 1986,
Bond et al 1986,
Wright & Malkan 1987,
Lacey & Field 1988,
Adams et al 1989,
Draine & Shapiro 1989).
Such dust could either be
pregalactic in origin or confined to galaxies themselves if galaxies
cover the
sky. If the dust cross-section for photons of wavelength
 is assumed to be
geometric (
is assumed to be
geometric ( r2d for a grain radius
rd) for
r2d for a grain radius
rd) for
 >>
rd, but to fall off as
>>
rd, but to fall off as
 -1 for
-1 for
 >>
rd then the spectrum should peak at a present wavelength
(Bond et al 1986)
>>
rd then the spectrum should peak at a present wavelength
(Bond et al 1986)
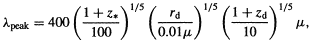
| (8.2) |
where zd is the epoch of dust production and we have
used Equation (8.1) with

 0.1 to express
0.1 to express
 R in
terms of z*. The crucial point is that the
wavelength is
very insensitive to the various parameters appearing in Equation (8.2)
because
the exponents are so small. At one time the Nagoya-Berkeley experiment
(Matsumoto et al 1984
appeared to indicate a submillimeter excess peaking
at almost exactly the wavelength predicted. However, the Nagoya-Berkeley
excess has now been disproved by FIRAS and the question arises of
whether
the VMO-plus-dust scenario is still compatible with COBE results.
R in
terms of z*. The crucial point is that the
wavelength is
very insensitive to the various parameters appearing in Equation (8.2)
because
the exponents are so small. At one time the Nagoya-Berkeley experiment
(Matsumoto et al 1984
appeared to indicate a submillimeter excess peaking
at almost exactly the wavelength predicted. However, the Nagoya-Berkeley
excess has now been disproved by FIRAS and the question arises of
whether
the VMO-plus-dust scenario is still compatible with COBE results.
It should be stressed that one does not necessarily expect dust reprocessing
anyway. Pregalactic dust with density
 d would
only absorb UV photons for
d would
only absorb UV photons for
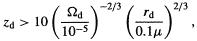
| (8.3) |
where  d
is normalized to the sort of value appropriate for galaxies. It is not
clear whether this condition can be satisfied. One has no direct
evidence for
pregalactic dust but in any hierarchical clustering picture one would
expect at least some pregalactic dust production
(Najita et al 1990).
For example, one
could envisage the dust produced by the first dwarf galaxies being blown
into
intergalactic space because the gravitational potential of the dwarfs
would be
so small. The dust in galaxies themselves would suffice to reprocess the VMO
background only if galaxies cover the sky which - for galaxies like our own
- requires the redshift of galaxy formation to exceed about 10
(Ostriker & Heisler 1984,
Heisler & Ostriker 1988,
Ostriker et al 1990).
Even if galaxies do cover the sky, the analysis of
Fall et al (1989)
indicates that the dust-to-gas ratio in
primordial galaxies may only be 5-20% that of the Milky Way for 2 <
z < 3,
which makes the opaqueness condition difficult to satisfy.
d
is normalized to the sort of value appropriate for galaxies. It is not
clear whether this condition can be satisfied. One has no direct
evidence for
pregalactic dust but in any hierarchical clustering picture one would
expect at least some pregalactic dust production
(Najita et al 1990).
For example, one
could envisage the dust produced by the first dwarf galaxies being blown
into
intergalactic space because the gravitational potential of the dwarfs
would be
so small. The dust in galaxies themselves would suffice to reprocess the VMO
background only if galaxies cover the sky which - for galaxies like our own
- requires the redshift of galaxy formation to exceed about 10
(Ostriker & Heisler 1984,
Heisler & Ostriker 1988,
Ostriker et al 1990).
Even if galaxies do cover the sky, the analysis of
Fall et al (1989)
indicates that the dust-to-gas ratio in
primordial galaxies may only be 5-20% that of the Milky Way for 2 <
z < 3,
which makes the opaqueness condition difficult to satisfy.
In general, one would expect there to be both a far-IR dust background and
a near-IR attenuated starlight background, with the relative intensity
reflecting
the efficiency of dust reprocessing. By changing the amount of dust, one can
redistribute the light between the near-IR and far-IR in an attempt to
obviate
the constraints. In order to examine the issue in more detail,
Bond et al (1991)
have carried out a more sophisticated analysis, in which the dust cross
section is assumed to scale as
 -
- at infrared
wavelengths. They also introduce a more
realistic model for the source luminosity history, allowing for both
"burst" and
"continuous" models. Comparison with the far-IR and COBE
constraints is
shown in Figure 6 for two of their
models with
at infrared
wavelengths. They also introduce a more
realistic model for the source luminosity history, allowing for both
"burst" and
"continuous" models. Comparison with the far-IR and COBE
constraints is
shown in Figure 6 for two of their
models with  = 1.5 and
z* = 100. One
has
= 1.5 and
z* = 100. One
has  d =
10-5 and zd = 50 (which is above the
FIRAS constraint); the other
has
d =
10-5 and zd = 50 (which is above the
FIRAS constraint); the other
has  d =
10-6 and zd = 10 (which is below it). This
shows that the
VMO-plus-dust scenario is only viable for models with a high redshift of
energy
release (z* = 100) and small amounts of dust
(
d =
10-6 and zd = 10 (which is below it). This
shows that the
VMO-plus-dust scenario is only viable for models with a high redshift of
energy
release (z* = 100) and small amounts of dust
( d =
10-6). Of the models
considered by
Bond et al (1991),
Wright et al (1994)
claim that only their model 12 still survives.
d =
10-6). Of the models
considered by
Bond et al (1991),
Wright et al (1994)
claim that only their model 12 still survives.