Annu. Rev. Astron. Astrophys. 1994. 32: 531-590 Copyright © 1994 by Annual Reviews. All rights reserved

8.4. Gravitational Radiation from Black Holes

The formation of a population of black holes of mass M at redshift z_B would be expected to generate bursts of gravitational radiation with a characteristic period and duration:

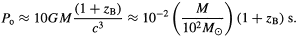
(8.4)

One can show that the expected time between bursts (as seen today) is less than their characteristic duration provided that _B > 10^-2-2, where is the total density parameter. (Bertotti & Carr 1980). If the holes make up galactic halos, one would therefore expect the burst to form a background of waves with present density _g = _gB(1 + z_B)^-1, where _g is the efficiency with which the collapsing matter generates gravity waves. If _g were as high as 0.1, the background could be detectable by ground-based laser interferometers (e.g. LIGO) for M below 10³ M, by Doppler tracking of interplanetary spacecraft (e.g. Cassini) for M in the range 10⁵-10¹⁰ M, and by pulsar timing for M above 10⁹ M. The observable domains are indicated in Figure 7 and the dotted lines indicate how the predicated backgrounds depend on M and z_B. Note that the value of _g is very uncertain and it is probably well below 0.1 for isolated collapse.

The prospects of detecting the gravitational radiation would be much better if the holes formed in binaries (Bond & Carr 1984). This is because two sorts of radiation would then be generated: (a) continuous waves as the binaries spiral inward due to quadrupole emission; and (b) a final burst of waves when the components finally merge. The burst would have the same characteristics as that associated with isolated holes but it would be postponed to a lower redshift and _g would be larger (~ 0.08) because of the larger asymmetry; both factors would increase _g. The continuous waves would also be interesting since they would extend the spectrum to longer periods, thus making the waves detectable by a wider variety of techniques. Over most wavebands, the spectrum of the waves would be dominated by binaries whose initial separation is such that they are coalescing at the present epoch. This corresponds to a separation a_crit = 10² (M/10² M)^3/4 R. The total background generated by the binaries is also shown in Figure 7: For each value of M, _g(P) goes as P^-2/3, as indicated by the broken lines. Providing the fraction of binaries f_crit with around the critical separation is not too small, the background should be detectable by LIGO for M < 10³ M, by Cassini for 10⁵ M < M < 10¹⁰ M, by LISA for M < M < 10¹⁰ M, and by pulsar timing for M > 10⁶ M.

Figure 7. The spectrum of background gravitational waves generated by isolated black holes and coalescing binary black holes. In the first case, we assume that the holes have B = 1 and that they form at a redshift z*. In the second case, we assume that the binaries have the separation acrit such that they coalesce at the present epoch. Also shown are the (g, P) domain accessible 10 ground-based interometry, Doppler tracking of interplanetary spacecraft, pulsar timing, and space-based interferometry.

One could also hope to observe coalescences occurring at the present epoch. For our own halo, the average time t_burst between bursts and their expected amplitude h_burst would be

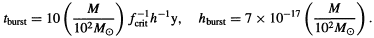
(8.5)

Although the time would be uncomfortably long, one could also detect bursts from the Virgo cluster every 4(M / 10² M) days with somewhat improved sensitivity. Haehnelt (1994) has argued that LISA could detect coalescence bursts throughout the Universe for M in the range 10³-10⁶ M.