Annu. Rev. Astron. Astrophys. 1984. 22: 157-184 Copyright © 1984 by Annual Reviews. All rights reserved

2. BASIC RESULTS

2.1. The Nature of Redshift

The standard theory assumes that electromagnetic radiation ("light" for short) travels on null geodesics (x^a() : k^a_{; b}k^b = 0, k^ak_a = 0, where k^a dx^a / d) in the space-time of general relativity and is characterized by the relations c = v, E = h, relating the wavelength , frequency , speed c, and energy E of a photon. Then the redshift z / (where is the change in wavelength measured from spectra for light emitted at wavelength ) is a direct consequence of measurable time dilation between the source and the observer (25, 91, 111). There can be various sources for this time dilation.

In the cosmological context, there is assumed to be a well-defined average motion of matter at each point in the Universe, representing the "standard" motion of matter there (24, 25); galaxies moving in this standard way, characterized by a four-velocity u^a (where u_a u^a = - 1), are called "fundamental particles," and an observer moving with four-velocity u^a is denoted as a "fundamental observer." The cosmological redshift z_c is the redshift observed when both the source and observer move with this velocity (at their respective space-time positions) and there are no local gravitational redshift effects. However, there will be local Doppler redshifts z_Ds, z_Do if the source or observer is not moving at the standard velocity, and there may be local gravitational redshifts z_Gs, z_Go generated at the source or the observer by local gravitational potential wells. (Notice that in each case the effect could be a blueshift rather than redshift; this corresponds to a negative value of z, and we shall assume this possibility without explicitly mentioning it.) These contributions to the total redshift z are not distinguishable from each other by any direct measurement of the received radiation; the measurable quantity is the total redshift z, given in terms of the other quantities by

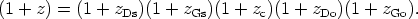
(1)

The cosmological redshift depends on the path of the light ray from the source to the observer. One can distinguish two contributions. The first arises from the increase in relative distance of fundamental observers due to integrated local relative motion of matter [characterized by the expansion tensor _ab = h_a^c h_b^au_{(c; d)} (24, 25), where h_ab g_ab + u_au_b projects into the rest-space orthogonal to u^a]. The second arises from the noninertial motion of the fundamental observers, characterized by a nonzero acceleration vector 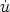^a u^a_{; b} u^b (indicating that their world-lines are nongeodesic). The change of redshift when moving a distance dl, measured by a fundamental observer along a null geodesic in direction e^a = h_b^a k^b / (u_ck^c), obeys the equation (24, 25)

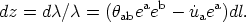
(2a)

Thus one can write

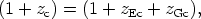
(2b)

where z_Ec is the usual Hubble (expansion) term (obtained by integrating the first term in Equation 2a), and z_Gc is what might be termed a "cosmological gravitational redshift" (obtained by integrating the second term).

In the FLRW models, it is assumed that the other redshift contributions are very small compared with the basic cosmological expansion effect. Then

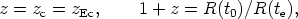
(3)

where R(t) is the "radius function" of the Universe that represents the time behavior of the distance between any pair of fundamental particles as the Universe evolves (by the homogeneity and isotropy of these models, the distances between all pairs of fundamental particles scale in the same way); and t_e, t₀ are the times of emission and observation of the light, respectively. The observation of systematic redshifts indicates that the Universe is expanding at the present time t₀; so H₀ (R ^-1 dR / dt)|₀ > 0.