Annu. Rev. Astron. Astrophys. 1984. 22: 157-184 Copyright © 1984 by Annual Reviews. All rights reserved

2.2. Basic Equations

The standard results rest on three pillars: the conservation equations, the Raychaudhuri equation, and the energy conditions. The form of these equations depends on the nature of the matter in the Universe. It is assumed here that the usual description of matter on a cosmological scale as a "perfect fluid" is adequate at most times. Then (24, 25) the stress tensor of each component of matter or energy present takes the form

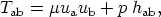
(4a)

where µ is the (relativistic) energy density of the fluid and p its pressure. To complete the description of matter, we must give suitable equations of state for the matter variables; in the hot early Universe, the "standard" theory assumes (except during phases of pair annihilation) that these are

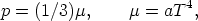
(4b)

describing a "Fermi gas" with temperature T (107, 109).

THE CONSERVATION EQUATIONS     The stress tensor T_ab of matter that does not interact with other matter or radiation obeys the equations T^db_; b = 0. If this matter is a perfect fluid (Equation 4a), the energy conservation equation u_dT^db_; b = 0 takes the form

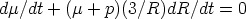
(5)

where t is proper time measured along the fluid flow lines, showing the effect of expansion or compression of the matter on its energy density. (The radius R is related to the volume V of a fluid element by the relation V R³.) The momentum conservation equation h_d^aT^db_; b = 0 is

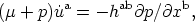
(6)

which shows how spatial pressure gradients generate acceleration (and thus observable gravitational redshifts).

THE RAYCHAUDHURI EQUATION     Contracting the Ricci identity u^a_; bc - u^a_; cb = R^a_dbcu^d for u^a and using Einstein's field equations

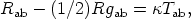
(7)

it follows that the volume behavior of the fluid is controlled by the Raychaudhuri equation (82, 24, 25, 45)

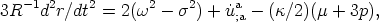
(8)

where ² is the squared magnitude of the fluid vorticity and ² the squared magnitude of the shear (or rate of distortion). Because d²R / dt² is the curvature of the curve R(t), this equation shows how rotation tends to hold matter apart and distortion to make it collapse, with (µ + 3p) the "active gravitational mass density" that tends to cause collapse.

ENERGY CONDITIONS     Various "energy conditions" have been proposed as physical restrictions on the matter (45); for present purposes, the major such conditions are

(9a) (9b)

with Equation 9a needed for physical stability of matter (as follows from Equations 5 and 6) and Equation 9b implying that the gravitational effect of matter is attractive (see Equation 8). It is usually assumed that "reasonable" matter obeys these conditions.