Annu. Rev. Astron. Astrophys. 1984. 22: 157-184 Copyright © 1984 by Annual Reviews. All rights reserved

4.2. Alternative Gravity

CLASSICAL THEORIES     There are a large variety of classical (i.e. non-quantum) theories of gravity proposed as alternatives to the general theory of relativity (36, 112). In each case, one can work out the corresponding application of the theory to the Robertson-Walker metrics and so obtain a corresponding version of the origin of the Universe.

Many of these alternative theories can be written as close variants of general relativity, with field equations of the form

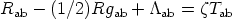
(15)

for some suitable choice of _ab and [which will be given in terms of other auxiliary fields, e.g. the scale function in scale-covariant theories such as the Brans-Dicke theory (12, 106, 109), the creation field C in the original Hoyle-Narlikar theory (46, 109), or the second metric _ab in Rosen's bimetric theory (87, 88); these auxiliary fields will satisfy their own field equations]. Now just as in the transition from Equation 12 to Equation 13, one can rewrite this equation in the form

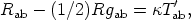
(16a)

where

(16b)

that is, we can regard the new theory as described by Einstein's equations with a new form of matter. Although T_ab satisfies the energy condition (Equation 9b), T'_ab may not; if so, one may (as in the case of alternative matter) find cosmological solutions with a nonsingular origin. A further feature is now of importance. As is well known, the tensor (R_ab - (1/2)Rg_ab) has vanishing divergence; and indeed this fact is responsible for the standard form of the field equations (Equation 7). Equations 15 and 16 show that

(17a) (17b)

Now _ab may have a nonzero divergence or _{; b}T^ab may be nonzero. Thus, although T'_ab satisfies the conservation equations, in general T_ab does not, so the energy or momentum of the matter fields are not conserved in this theory; this is the origin of the possibility of matter creation in theories such as the Hoyle-Narlikar theory. However, one should note the comment by Lindblom & Hiscox (52): This procedure effectively constructs non-conserved quantities within a conservative theory. One can rewrite such theories in conservative form by putting the equations in the form of Equation 16 (cf. 61).

If an alternative theory of gravity leads to sufficiently large equivalent energy condition violations, a singularity can be avoided. This is possible, for example, in the Hoyle-Narlikar theory (46), in theories with torsion (83, 105), and in bimetric theories (80, 87). If the gravitational field equations are derived from a Lagrangian more complex than the general relativity Lagrangian, in general we may expect energy violations to be possible. Thus, if we introduce terms quadratic in the curvature invariants, a "bounce" may be possible (67); when nonlinear Lagrangians are considered that are arbitrary functions f (R) of the scalar curvature R, the singularity can be avoided through a suitable choice of f (R) (4, 50); and if the singularity is not avoided, one may nevertheless avoid the occurrence of horizons (4). Again, if the matter fields are nonminimally coupled to the curvature, singularity avoidance is, in general, possible (71).

CONFORMAL THEORIES     A class of alternative theories that have attracted particular attention are the variable-G or scale-covariant theories, such as Diracs theory (21), the Brans-Dicke theory, the later Hoyle-Narlikar theories, and the theory of Canuto and coworkers. In general, different conformal gauges can be chosen in these theories that relate different metric representations through appropriate choice of a conformal factor (15, 89). This allows alternative explanations for observed redshifts; effectively one can switch terms in Equations 1 and 2, for when conformal transformations are allowed, one can no longer clearly distinguish between expansion and acceleration of the fundamental particles. [These depend on the conformal frame used (66).] In fact, conformal transformations can be used to transform the isotropic expansion of FLRW fundamental observers to zero; so one can remove the singularities in the matter flow in FLRW models by appropriate conformal transformation, i.e. by appropriate choice of a conformal frame. (In fact, it is well known that all the FLRW universe models are conformal both to flat space-time and to the Einstein static universe.) The effective matter tensor in the field equations (Equation 16) will therefore, in general, violate the energy conditions, for this is what makes it possible to transform the expansion to zero without violating the Raychaudhuri equation. This may explicitly be seen to be true in the revised Dicke theory for (2 + 3) < 0 (83). It is therefore not surprising that in some cases the massless scalar field in the Brans-Dicke theory can prevent the occurrence of initial singularities in the Universe (37). The remarks above lead us to expect that this will be a general feature of gauge-covariant theories.

QUANTUM COSMOLOGY     When investigating the behavior of the Universe at very early times, a quantum cosmological model may be used to take quantum gravitational effects into account; however, the construction of such models is considerably hampered by the lack of a complete and manageable quantum theory of gravity. Space limitations do not allow an adequate discussion of such models in this article; rather, the reader is referred to a recent excellent review article and the references therein (43).

Overall, it is easy to find alternative theories of gravitation where energy violation may occur. There is no compelling reason to support these theories against general relativity, except that it is clear that in the high-density and curvature limit a quantum theory of gravity is ultimately needed. Thus the quantum cosmology results (when agreement is reached on them) are clearly of considerable significance for any discussion of the origin of the Universe. Singularities might be avoided in the quantum case, but if not, it seems possible that they will be less severe than in the classical case; and at least horizons may not occur in these models.