Copyright © 1984 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1984. 22:
157-184 Copyright © 1984 by Annual Reviews. All rights reserved |
There are two basically different variations of the standard FLRW geometries: models that are spatially homogeneous but anisotropic, and models that are spatially inhomogeneous.
The family of spatially homogeneous but anisotropic evolving universe models have been extensively studied (see 49, 55, 56 for recent reviews). While these universes may at some stage in their history be very similar to the FLRW universes, they can have totally different singularity structures. The kinds of singularity that can occur depend on whether the universes are orthogonal or tilted.
ORTHOGONAL UNIVERSES These are spatially homogeneous universes in which the matter flow vector is orthogonal (in the space-time sense) to the surfaces of homogeneity; thus, there is no motion of the matter relative to these homogeneous space sections. The fluid flow is geodesic and rotation free, and the surfaces of homogeneity are surfaces of simultaneity for all the fundamental observers. The models comprise Bianchi orthogonal models (the general case) and Kantowski-Sachs universes (a special "rotationally symmetric" case).
In all these cases, because
 =
=
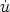 a = 0, the
existence of a singularity
follows directly from the energy conditions (Equation 9) and the
Raychaudhuri equation (Equation 8); in essence, the Raychaudhuri
equation shows that the normals to the surfaces of homogeneity must
approach a point of intersection, but the fluid is moving along these
normals and so runs into a singularity where the density of matter
diverges. (2)
The existence of the distortion term
a = 0, the
existence of a singularity
follows directly from the energy conditions (Equation 9) and the
Raychaudhuri equation (Equation 8); in essence, the Raychaudhuri
equation shows that the normals to the surfaces of homogeneity must
approach a point of intersection, but the fluid is moving along these
normals and so runs into a singularity where the density of matter
diverges. (2)
The existence of the distortion term
 2 in Equation
8 shows
that the singularity is in general worse than in the FLRW case; indeed,
usually the singularity is shear dominated, the effect of the matter
term being negligible at early times. Limits on the amount of anisotropy
come from observed limits on the anisotropy of the CMBR and from
observed light-element abundances, compared with model predictions
(55,
89,
100).
2 in Equation
8 shows
that the singularity is in general worse than in the FLRW case; indeed,
usually the singularity is shear dominated, the effect of the matter
term being negligible at early times. Limits on the amount of anisotropy
come from observed limits on the anisotropy of the CMBR and from
observed light-element abundances, compared with model predictions
(55,
89,
100).
In these models, many different kinds of singularity structure can occur. In the simplest (Bianchi I) case, the solution resembles the vacuum Kasner solution; the singularity may be a "cigar" or "pancake" singularity (55, 100). If the cigar singularity occurs, horizons are broken in one spatial dimension (45, 64). Generically (in Bianchi VIII or IX) there will be oscillatory behavior, with a series of Kasner-like epochs taking place between "bounces" off a potential wall (7, 64). These possibilities have been discussed in a previous volume of this series (72). It seems agreed that the oscillatory behavior continues right back to the origin of the Universe, so that the initial behavior of the models can be characterized in a strict sense as "chaotic" (3); unfortunately, this does not suffice to break the horizons in all directions, as was once hoped (57).
While these singularities are geometrically quite different from the SHBB through their anisotropic expansion (and in many cases oscillatory behavior), which modifies (A), the essential features (B) remain; the most significant difference is the possibility of horizon breaking in some directions [so that (C) no longer holds in all directions].
TILTED UNIVERSES In this case, the surfaces of homogeneity are not orthogonal to the matter flow. Thus, although they are strictly spatially homogeneous in a rigorous sense, these universes appear inhomogeneous to the fundamental observers, who move relative to the homogeneous spatial sections (35). One can view this either as a result of their surfaces of instantaneity not coinciding with the surfaces of homogeneity (51) or because Doppler effects due to the peculiar velocity of the observer make a uniform distribution of matter appear anisotropic (30).
In tilted universes the matter can move with vorticity and will have nonzero acceleration unless the pressure is constant. Thus, the Raychaudhuri equation for the fluid no longer directly implies that a singularity occurs. However, the Raychaudhuri equation for the normals to the surfaces of homogeneity implies that these normals become singular within a finite proper distance; this result shows that the spatially homogeneous part of the Universe must end within a finite time. A careful analysis then demonstrates that the Universe must be singular at this time (45).
There are two rather different ways the spatially homogeneous region of the Universe can end in the past. (a) The first possibility is that an infinite density (spatially homogeneous) singularity can bound this region; then the situation is essentially the same as in the case of the orthogonal universes, except that the geometry can be more complex (because of the rotation and acceleration of the matter). The Universe originates at this infinite density singularity. (b) The second possibility (94) is that the density is finite at the boundary of the spatially homogeneous region of space-time (which represents late times in the Universe). The matter originates at early times in a spatially inhomogeneous, stationary region of space-time, separated from the spatially homogeneous region by a (Cauchy) horizon (18, 31).
It is easiest to understand this situation as follows
(26,
27):
consider the action of boosts of the Lorentz group through a hyperbolic
angle  in
two-dimensional Minkowski space-time
(Figure 1a). If a single
matter flow line through the origin P is spread over the
space-time by repeating this action infinitely often, the (infinite)
family of flow lines thus generated intersect at P and we have a
model of Case (a): the
spatially homogeneous region I comes to an end at a boundary where the
matter density is infinite. This region comprises the entire Universe
(Figure 1b). Suppose, however, a single
flow line of matter that crosses
from region I to region II is spread around by the same action of the
Lorentz group. Then the surfaces of constant density change from being
spacelike to being timelike as the fluid crosses the horizon
H-1(
in
two-dimensional Minkowski space-time
(Figure 1a). If a single
matter flow line through the origin P is spread over the
space-time by repeating this action infinitely often, the (infinite)
family of flow lines thus generated intersect at P and we have a
model of Case (a): the
spatially homogeneous region I comes to an end at a boundary where the
matter density is infinite. This region comprises the entire Universe
(Figure 1b). Suppose, however, a single
flow line of matter that crosses
from region I to region II is spread around by the same action of the
Lorentz group. Then the surfaces of constant density change from being
spacelike to being timelike as the fluid crosses the horizon
H-1( )
(Figure 1c), so while the late part I of
the model is spatially
homogeneous as before, the early part II is spatially inhomogeneous.
This provides a model of Case (b). The limiting value of the
density at
the boundary of these regions of space-time, shown by a zigzag line in
Figure 1c, is finite: it is the same as
the density on the horizon
H-1(
)
(Figure 1c), so while the late part I of
the model is spatially
homogeneous as before, the early part II is spatially inhomogeneous.
This provides a model of Case (b). The limiting value of the
density at
the boundary of these regions of space-time, shown by a zigzag line in
Figure 1c, is finite: it is the same as
the density on the horizon
H-1( )
(which is a surface of homogeneity). However, the Universe cannot be
extended beyond this boundary, for a singularity occurs here. One can
see this by noting that in Figure 1c the
light cone of any point
is at 45°. The past null geodesic to the left from any point in the
space-time
runs into the boundary in a finite distance, but in that distance it
crosses an infinite number of world lines. Consequently, the density of
matter measured in a frame of vectors parallel propagated down this null
geodesic will diverge. This parallel-propagated frame is related to a
group-invariant frame by a Lorentz transformation that diverges at the
boundary; and the density is perfectly finite at each point if measured
in this group-invariant frame. Thus, this singularity is a nonscalar
singularity (45)
[colloquially known as a "Whimper"
(31)].
All curvature
and matter invariants are regular as one approaches the boundary; the
divergence occurs when the Ricci and matter tensors are measured in a
parallel-propagated frame.
)
(which is a surface of homogeneity). However, the Universe cannot be
extended beyond this boundary, for a singularity occurs here. One can
see this by noting that in Figure 1c the
light cone of any point
is at 45°. The past null geodesic to the left from any point in the
space-time
runs into the boundary in a finite distance, but in that distance it
crosses an infinite number of world lines. Consequently, the density of
matter measured in a frame of vectors parallel propagated down this null
geodesic will diverge. This parallel-propagated frame is related to a
group-invariant frame by a Lorentz transformation that diverges at the
boundary; and the density is perfectly finite at each point if measured
in this group-invariant frame. Thus, this singularity is a nonscalar
singularity (45)
[colloquially known as a "Whimper"
(31)].
All curvature
and matter invariants are regular as one approaches the boundary; the
divergence occurs when the Ricci and matter tensors are measured in a
parallel-propagated frame.
This model gives a good representation of what happens in the full
four-dimensional Case (b) tilted Bianchi cosmologies. The spatially
homogeneous region is bounded by a Whimper singularity on the one hand,
and a Cauchy horizon
H-1( ) on
the other; the fluid crosses the Cauchy
horizon from an earlier spatially inhomogeneous region, which is also
partially bounded by the Whimper singularity. This singularity is
causally null; correspondingly
(45,
75),
there will be no particle
horizon in the direction of the Whimper singularity (but there will be
one in the opposite direction; cf. the causal diagrams in
18). It is a
"mild" singularity in that the temperature and density of the matter is
finite there. The fluid itself originates at a second singularity (not
shown in Figure 1c) that is
timelike. Here, in general, the density will
diverge, but this will not always be the case: situations are known
(18)
where the density is finite at this initial singularity (but where the
conformal geometry is singular). Thus, in such exact solutions of
Einstein's equations - which have reasonable equations of state and obey
the energy conditions - two singularities occur, but there is a finite
maximum density for matter in the Universe; hence, there is also a bound
to the temperature that will occur.
) on
the other; the fluid crosses the Cauchy
horizon from an earlier spatially inhomogeneous region, which is also
partially bounded by the Whimper singularity. This singularity is
causally null; correspondingly
(45,
75),
there will be no particle
horizon in the direction of the Whimper singularity (but there will be
one in the opposite direction; cf. the causal diagrams in
18). It is a
"mild" singularity in that the temperature and density of the matter is
finite there. The fluid itself originates at a second singularity (not
shown in Figure 1c) that is
timelike. Here, in general, the density will
diverge, but this will not always be the case: situations are known
(18)
where the density is finite at this initial singularity (but where the
conformal geometry is singular). Thus, in such exact solutions of
Einstein's equations - which have reasonable equations of state and obey
the energy conditions - two singularities occur, but there is a finite
maximum density for matter in the Universe; hence, there is also a bound
to the temperature that will occur.
The plausibility of these universe models rests on their ability to give reasonable predictions for element production and compatibility with the microwave anisotropy. Initial investigation (31, 60) is encouraging; it seems that current observational evidence is quite compatible with such singularities. It should be mentioned that it is known that these models are of zero measure in the set of all spatially homogeneous models (95, 96), and this fact has been used as an argument against their occurrence. While this is an interesting line of argument, its status is unclear because of the uniqueness of the Universe. Additionally, it should be mentioned that if one pursues this line, the SHBB FLRW models are an even smaller subset of the spatially homogeneous models and thus, according to this argument, are even more unlikely to occur than the Whimpers.
OTHER EFFECTS As in the previous case, one can consider spatially homogeneous, anisotropic universes with other equations of state or governed by other gravitational theories. Because of the shear in these cosmologies, in many cases (e.g. for orthogonal fluids) one may expect the singularities to be worse than in corresponding FLRW universes. Thus, for example, while torsion can prevent singularities in FLRW universes, it cannot do so in Bianchi I universes (99).
Where quantum field effects seem to make a significant difference is in the evolution forward in time from the singularity; for in anisotropic universes there will be significant pair creation of conformally invariant particles, and this will dissipate anisotropy and so drive the Universe toward a state of isotropy (43, 115). Similarly, the effect of a false-vacuum inflationary expansion in a Bianchi universe will be to make it evolve exponentially toward the de Sitter (isotropic) solution (108). However, if the anisotropy in the Universe is too large at the end of the quantum gravity era, the inflationary phase will never take place (5a). Thus, quantum effects can contribute to a limited extent toward Misner's (63) vision of a situation where any anisotropy or nonuniformity will be dissipated by physical processes in the early Universe, so giving an "explanation" of presently observed isotropy.
2 See (18) for a careful discussion of the Bianchi cases and (16) for the Kantowski-Sachs case. Back.