CHAPTER 1
THE RECENT HISTORY OF COSMIC MAGNETIC FIELDS

The main observational tracers of galactic and extra-galactic magnetic fields are (comprehensive reviews of the subject can be found in Refs. [1, 2]): the Zeeman splitting of spectral lines; the intensity and the polarization of synchrotron emission from free relativistic electrons; the Faraday rotation measurements (RMs) of polarized electromagnetic radiation passing through a ionized medium.

Typically the Zeeman splitting, though direct, is too small to be useful outside our galaxy. Unfortunately, although the synchrotron emission and RMs allows to trace magnetic fields in very distant objects, both kind of measurements requires an independent determination of the local electron density n_e. This is sometimes possible, e.g. by studying the X-ray emission from the electron gas when this is very hot, typically when this is confined in a galaxy cluster. Otherwise n_e may be not always easy to determine, especially for very rarefied media like the intergalactic medium (IGM). In the case of synchrotron emission, which intensity is proportional to n_e B², an estimation of B is sometimes derived by assuming equipartition between the magnetic and the plasma energy densities.

If the magnetic field to be measured is far away one relies on Faraday rotation. The agreement generally found between the strength of the field determined by RMs and that inferred from the analysis of the synchrotron emission in relatively close objects gives reasonable confidence on the reliability of the first method also for far away systems. It should be noted, however, that observations of synchrotron emission and RMs are sensitive to different spatial components of the magnetic field [2]. The RM of the radiation emitted by a source with redshift z_s is given by

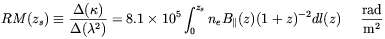
(1.1)

where B is the field strength along the line of sight and

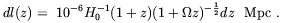
(1.2)

H₀ is the Hubble constant. The previous expression holds for a vanishing cosmological constant and modification for finite is straightforward. This method requires knowledge of the electron column and possibility of field reversals. For nearby measurements in our own galaxy pulsar frequency and their decays can pin down these effects. Otherwise these stars are too far to help. For this reason to determine the magnetic field of the IGM by Faraday RMs is quite hard and only model dependent upper limits are available.

We now briefly summarize the observational situation.

Magnetic fields in galaxies. The interstellar magnetic field in the Milky Way has been determined using several methods which allowed to obtain valuable information about the amplitude and spatial structure of the field. The average field strength is 3-4 µG. Such a strength corresponds to an approximate energy equipartition between the magnetic field, the cosmic rays confined in the Galaxy, and the small-scale turbulent motion [1]

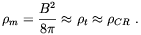
(1.3)

Remarkably, the magnetic energy density almost coincides with energy density of the cosmic microwave background radiation (CMBR). The field keeps its orientation on scales of the order of few kiloparsecs (kpc), comparable with the galactic size, and two reversals have been observed between the galactic arms, suggesting that the Galaxy field morphology may be symmetrical. Magnetic fields of similar intensity have been observed in a number of other spiral galaxies. Although equipartition fields were observed in some galaxies, e.g. M33, in some others, like the Magellanic Clouds and M82, the field seems to be stronger than the equipartition threshold. Concerning the spatial structure of the galactic fields, the observational situation is, again, quite confused with some galaxies presenting an axially symmetrical geometry, some other a symmetrical one, and others with no recognizable field structure [2].

Magnetic fields in galaxy clusters. Observations on a large number of Abel clusters [3], some of which have a measured X-ray emission, give valuable information on fields in clusters of galaxies. The magnetic field strength in the inter cluster medium (ICM) is well described by the phenomenological equation

(1.4)

where L is the reversal field length and h₅₀ is the reduced Hubble constant. Typical values of L are 10-100 kpc which correspond to field amplitudes of 1-10 µG. The concrete case of the Coma cluster [4] can be fitted with a core magnetic field B ~ 8.3 h₁₀₀^1/2 G tangled at scales of about 1 kpc. A particular example of clusters with a strong field is the Hydra A cluster for which the RMs imply a 6 µG field coherent over 100 kpc superimposed with a tangled field of strength ~ 30 µG [5]. A rich set of high resolution images of radio sources embedded in galaxy clusters shows evidence of strong magnetic fields in the cluster central regions [6]. The typical central field strength ~ 10 - 30 µG with peak values as large as ~ 70 µG. It is noticeable that for such large fields the magnetic pressure exceeds the gas pressure derived from X-ray data suggesting that magnetic fields may play a significant role in the cluster dynamics. It is interesting, as it has been shown by Loeb and Mao [7] that a discrepancy exists between the estimate of the mass of the Abell cluster 2218 derived from gravitational lensing and that inferred from X-ray observations which can be well explained by the pressure support produced by a magnetic fields with strength ~ 50 µG. It is still not clear if the apparent decrease of the magnetic field strength in the external region of clusters is due to the intrinsic field structure or it is a spurious effect due to the decrease of the gas density. Observations show also evidence for a filamentary spatial structure of the field. According to Eilek [6] the filaments are presumably structured as a flux rope, that is a twisted field structure in which the field lies along the axis in the center of the tube, and becomes helical going away from the axis.

It seems quite plausible that all galaxy clusters are magnetized. As we will discuss in the next section, these observations are a serious challenge to most of the models proposed to explain the origin of galactic and cluster magnetic fields.

Magnetic fields in high redshift objects. High resolution RMs of very far quasars have allowed to probe magnetic fields in the distant past. The most significative measurements are due to Kronberg and collaborators (see Ref. [1] and Refs. therein). RMs of the radio emission of the quasar 3C191, at z = 1.945, presumably due a magnetized shell of gas at the same redshift, are consistent with a field strength in the range 0.4-4 µG. The field was found to maintain its prevailing direction over at least ~ 15 kpc, which is comparable with a typical galaxy size. The magnetic field of a relatively young spiral galaxy at z = 0.395 was determined by RMs of the radio emission of the quasar PKS 1229-021 lying behind the galaxy at z = 1.038. The magnetic field amplitude was firmly estimated to be in the range 1-4 µG. Even more interesting was the observation of field reversals with distance roughly equal to the spiral arm separation, in a way quite similar to that observed in the Milky Way.

Intergalactic magnetic fields. The radio emission of distant quasars is also used to constrain the intensity of magnetic fields in the IGM which we may suppose to pervade the entire Universe. As we discussed, to translate RMs into an estimation of the field strength is quite difficult for rarefied media in which ionized gas density and field coherence length are poorly known. Nevertheless, some interesting limits can be derived on the basis of well known estimates of the Universe ionization fraction and adopting some reasonable values of the magnetic coherence length. For example, assuming a cosmologically aligned magnetic field, as well as = 1, = 0, and h = 0.75, the RMs of distant quasar imply B_IGM 10^-11 G [1]. A field which is aligned on cosmological scales is, however, unlikely. As we have seen in the above, in galaxy clusters the largest reversal scale is at most 1 Mpc. Adopting this scale as the typical cosmic magnetic field coherence length and applying the RM(z_s) up to z_s ~ 2.5, Kronberg found the less stringent limit B_IGM 10^-9 G for the magnetic field strength at present time.

A method to determine the power spectrum of cosmic magnetic fields from RMs of a large number of extragalactic sources has been proposed by Kolatt [8]. The result of this kind of analysis would be of great help to determine the origin and the time evolution of these fields.

Another interesting idea proposed by Plaga [9] is unfortunately not correct. The idea here is to look to photons from an instantaneous cosmological source, like a gamma burst or a supernova, and check for the existence of a delayed component of the signal. This new component would be due to an original photon creating an electron positron pair and in turn the charged particle sending a photon in the original direction by inverse Compton scattering. For sources at cosmological distances the delay would be sensitive to a small B field, say 10^-11 G that would affect the motion of the charged intermediate particle. Unfortunately, the uncontrollable opening of the pair will produce a similar delay that cannot be disentangled from the time delay produced by the magnetic field.