1.2. The alternative: dynamo or primordial ?

For a long time the preferred mechanism to explain the aforementioned observations was the dynamo mechanism [10]. Today, however, new observational and theoretical results seems to point to a different scenario. Before trying to summarize the present status of art, a short, though incomplete, synthesis of what is a dynamo mechanism may be useful to some of our readers. More complete treatments of this subject can be found e.g. in Refs. [1, 11, 12, 13, 14].

A dynamo is a mechanism responsible for the conversion of kinetic energy of an electrically conducting fluid into magnetic energy. It takes place when in the time evolution equation of the magnetic field (see e.g. Ref. [15])

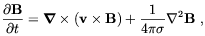
(1.5)

where s is the electric conductivity, the first term on the RHS of Eq. (1.5) (frozen-in term) dominates the second one which account for magnetic diffusion. As we will see in Sec. 1.4 this statement can be reformulated in terms of the magnetic Reynolds number which has to be much larger than unity. As it is clear from Eq. (1.5), a novanishing seed field is needed to initiate the dynamo process. Other three key ingredients are generally required. They are hydrodynamic turbulence, differential rotation and fast reconnection of magnetic lines. In the frozen-in limit magnetic lines are distorted and stretched by turbulent motion. It can be shown [13] that in the same limit the ratio B / of the magnetic field strength with the fluid density behaves like the distance between two fluid elements. As a consequence, a stretching of the field lines result in an increase of B. However, this effect alone would not be sufficient to explain the exponential amplification of the field generally predicted by the dynamo advocates. In fact, turbulence and global rotation of the fluid (e.g. by Coriolis force) may produce twisting of closed flux tubes and put both part of the twisted loop together, restoring the initial single-loop configuration but with a double flux (see Fig. 2 in Ref. [12]). The process can be iterated leading to a 2ⁿ-amplification of the magnetic field after the n-th cycle. The merging of magnetic loops, which produce a change in the topology (quantified by the so called magnetic helicity, see Sec. 1.4) of the magnetic field lines, requires a finite, though small, resistivity of the medium. This process occurs in regions of small extension where the field is more tangled and the diffusion time is smaller (see Sec. 1.4). As a consequence, the entire magnetic configuration evolves from a small-scale tangled structure towards a mean ordered one.

The most common approach to magnetic dynamo is the so called mean field dynamo. It is based on the assumption that fluctuations in the magnetic and velocity fields are much smaller of the mean slowly varying components of the corresponding quantities. Clearly, mean field dynamo is suitable to explore the amplification of large scale magnetic structures starting from small scale seed fields in the presence of a turbulent fluid. The temporal evolution of the mean component of the magnetic field is obtained by a suitable averaging of Eq. (5) (below, mean quantities are labelled by a 0 and random quantities by a 1)

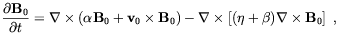
(1.6)

where

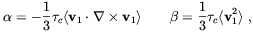
(1.7)

= 1 / 4 is the magnetic diffusivity, and _c is the correlation time for the ensemble of random velocities. The coefficient is proportional to the helicity h = <v₁ · × v₁ > of the flow; h measures the degree to which streamlines are twisted. A macroscopic parity violation is required to have h 0. One of the possible sources of this violation can be the Coriolis force produced by the rotation of the galaxy [11]. The term × ( × B₀) describes the additional field dissipation due to turbulent motion. Turbulence plays another crucial role in the generation of a toroidal component of the large scale magnetic fields which is essential for the stability of the entire field configuration [13]. Indeed the helicity, through the -term, is responsible for the generation of an electric field parallel to B₀ ⁽¹⁾. This field provides a mode for conversion of toroidal into poloidal magnetic field components. This is the so called -effect. To complete the "dynamo cycle" B_T B_P, another mechanism is required to convert the poloidal component into a toroidal one. This mechanism is provided by the differential rotation of the galactic disk which will wrap up the field line producing a toroidal field starting form a poloidal component; this is the -effect. The combination of the and effects gives rise to the, so called, - galactic dynamo. As a result of the coexistence of the poloidal and toroidal magnetic components, one of the main prediction of the of - dynamo is the generation of an axially symmetric mean fields.

In the case the term can be neglected, the solution of the mean field dynamo equation (1.6) can be written in the form [10]

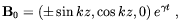
(1.8)

where z is the coordinate along the galaxy rotation axis, and = - k² ± k, k ~1 / L being the wavenumber. The field grows exponentially with time for non-zero helicity and if the scale L is sufficiently large. A general prediction of a dynamo mechanism is that amplification ends when equipartition is reached between the kinetic energy density of the small-scale turbulent fluid motion and the magnetic energy density. This correspond to a magnetic field strength in the range of 2-8 µG. Depending on the details of the model and of the local properties of the medium, the time required to reach saturation, starting from a seed magnetic fields with intensity as low as 10^-20 G, may be of 10⁸-10⁹ years. It should be noted that such an estimation holds under the assumption that the Universe is dominated by CDM with no cosmological constant. If, however, as recent observations of distant type-IA supernovae [16] and CMB anisotropy measurments [17] suggest, the Universe posses a sizeable cosmological constant, the available time for the dynamo amplification increases and a smaller initial seed field may be required. This point has been recently rised by Davis, Lilley and Törnkvist [18] who showed as the required seed field might be as low as 10^-30 G.

In the last decade the effectiveness of the mean field dynamo has been questioned by several experts of the field (for a recent review see Ref. [14]). One of the main arguments rised by these authors against this kind of dynamo is that it neglects the strong amplification of small-scale magnetic fields which reach equipartition, stopping the process, before a coherent field may develop on galactic scales.

The main, though not the unique, alternative to the galactic dynamo is to assume that the galactic field results directly from a primordial field which gets adiabatically compressed when the protogalactic cloud collapse. Indeed, due to the large conductivity of the intergalactic medium (see Sec. 1.4), magnetic flux is conserved in the intergalactic medium which implies that the magnetic field has to increase like the square of the size of the system l. It follows that

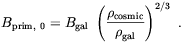
(1.9)

Since the present time ratio between the interstellar medium density in the galaxies and the density of the IGM is _IGM / _gal 10^-6, and B_gal ~ 10^-6 G, we see that the required strength of the cosmic magnetic field at the galaxy formation time (z ~ 5), adiabatically rescaled to present time, is

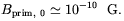
(1.10)

This value is compatible with the observational limit on the field in the IGM derived by RMs, with the big-bang nucleosynthesis constraints (see Chap. 3), and may produce observable effects on the anisotropies of the cosmic microwave background radiation (see Chap. 2). Concerning the spatial structure of the galactic field produced by this mechanism, differential rotation should wrap the field into a symmetric spiral with field reversal along the galactic disk diameter and no reversal across the galactic plane [2].

To decide between the dynamo and the primordial options astrophysicists have to their disposal three kind of information. They are:

• the observations of intensity and spatial distribution of the galactic magnetic fields;

• the observations of intensity and spatial distribution of the intergalactic magnetic fields;

• the observations of magnetic fields in objects at high redshift.

Observations of the magnetic field intensity in a some galaxies, including the Milky Way, show evidence of approximate equipartition between turbulent motion and magnetic energies, which is in agreement with the prediction of linear dynamo. There are however some exceptions, like the M82 galaxy and the Magellanic Clouds, where the field strength exceed the equipartition field. An important test concerns the parity properties of the field with respect to the rotations by about the galactic center. As we have discussed above, the primordial theory predicts odd parity and the presence of reversals with radius (a symmetric spiral field), whereas most dynamo models predict even parity (axially symmetric spiral) with no reversal. Although most galaxies exhibit no recognizable large-scale pattern, reversals are observed between the arms in the Milky Way, M81 and the high redshift galaxy discussed in the previous section, though not in M31 and IC342. Given the low statistical significance of the sample any conclusions are, at the moment, quite premature [2].

As we reported in the previous section only upper limits are available for the intensity of magnetic fields in the intergalactic medium. Much richer is the information that astrophysicists collected in the recent years about the magnetic fields in the inter-cluster medium (ICM). As we have seen, magnetic fields of the order of 1-10 µG seems to be a common features of galaxy clusters. The strength of these fields is comparable to that of galactic fields. This occurs in spite of the lower matter density of the ICM with respect to the density of interstellar medium in the galaxies. It seems quite difficult to explain the origin of the inter-cluster magnetic fields by simple ejection of the galactic fields. Some kind of dynamo process produced by the turbulent wakes behind galaxies moving in the ICM has been proposed by some authors but criticized by some others (for a review see Ref. [1]). This problem has become even more critical in light of recent high-precision Faraday RMs which showed evidence of magnetic fields with strength exceeding 10 µG in the cluster central regions. According to Kronberg [1], the observed independence of the field strength from the local matter density seems to suggest that galactic systems have evolved in a magnetic environment where B 1 µG. This hypothesis seems to be corroborated by the measurements of the Faraday rotations produced by high redshift protogalactic clouds. As we wrote in the previous section such measurements show evidence for magnetic fields of the order of 1 µG in clouds with redshift larger than 1. Since, at that time galaxies should have rotated few times, these observations pose a challenge to the galactic dynamo advocates. We should keep in mind, however, that galaxy formation in the presence of magnetic fields with strength 10^-8 G may be problematic due to the magnetic pressure which inhibits the collapse [19].

It is worthwhile to observe that primordial (or pre-galactic) magnetic fields are not necessarily produced in the early Universe, i.e. before recombination time. Several alternative astrophysical mechanisms have been proposed like the generation of the fields by a Biermann battery effect [20] (see also Ref. [1]). It has been suggested that the Biermann battery may produce seed fields which are successively amplified on galactic scale by a dynamo powered by the turbulence in the protogalactic cloud [14, 21]. This mechanism, however, can hardly account for the magnetic fields observed in the galaxy clusters. Therefore, such a scenario would lead us to face an unnatural situation where two different mechanisms are invoked for the generation of magnetic fields in galaxies and clusters, which have quite similar characteristics and presumably merge continuously at the border of the galactic halos.

Another possibility is that magnetic fields may have been generated by batteries powered by starbursts or jet-lobe radio sources (AGNs). In a scenario recently proposed by Colgate and Li [22] strong cluster magnetic fields are produced by a dynamo operating in the accretion disk of massive black holes powering AGNs. We note, however, that the dynamics of the process leading to the formation of massive black holes is still unclear and that preexisting magnetic fields may be required to carry away the huge angular moment of the in-falling matter (see e.g. Ref. [19]). For the same reason, preexisting magnetic fields may also be required to trigger starbursts (see the end of next section). This suggests that seed fields produced before recombination time may anyway be required.

In conclusion, although the data available today do not allow to answer yet to the question raised in this section, it seems that recent observations and improved theoretical work are putting in question the old wisdom in favour of a dynamo origin of galactic magnetic fields. Especially the recent observations of strong magnetic fields in galaxy clusters suggest that the origin of these fields may indeed be primordial.

Furthermore, magnetic fields with strength as large as that required for the primordial origin of the galactic fields through gravitational compression of the magnetized fluid, should give rise to interesting, and perhaps necessary, effects for structure formation. This will be the subject of the next section.

¹ Our readers with some experience in field theory may recognize that by producing parallel electric and magnetic fields the term is responsible of a sort of macroscopic CP violation. Back.