1.4. The evolution of primordial magnetic fields

A crucial issue for the investigation of a possible primordial origin of present time galactic and intergalactic magnetic fields is that concerning the time evolution of the magnetic fields in the cosmic medium. Three conditions are needed for the persistence of large static fields:

a) intrinsic stability of the field;

b) the absence of free charges which could screen the field;

c) to have a small diffusion time of the field with respect to the age of the Universe.

Condition a) does not hold for strong electric fields. It is a firm prediction of QED that an electric field decays by converting its energy in electron-positron pairs if e |E| m_e² [37, 38]. This, however, is a purely electric phenomenon. Although, at the end of the sixties, there was a claim that strong magnetic fields may decay through a similar phenomenon [39] the argument was proved to be incorrect. Only very strong fields may produce nontrivial instabilities in the QCD (if B > 10¹⁷ G) and the electroweak vacuum (if B > 10²³ G) which may give rise to a partial screening of the field. These effects (see Chap. 5) may have some relevance for processes which occurred at very early times and, perhaps, for the physics of very peculiar collapsed objects like magnetars [40]. They are, however, irrelevant for the evolution of cosmic magnetic fields after BBN time. The same conclusion holds for finite temperature and densities effects which may induce screening of static magnetic fields (see e.g. Ref. [41]).

Condition b) is probably trivially fulfilled for magnetic fields due to the apparent absence of magnetic monopoles in nature. It is interesting to observe that even a small abundance of magnetic monopoles at present time would have dramatic consequences for the survival of galactic and intergalactic magnetic fields which would lose energy by accelerating the monopoles. This argument was first used by Parker [42] to put a severe constraint on the present time monopole flux, which is F_M 10^-15 cm^-2 s^-1sr^-1. It was recently proposed by Kephart and Weiler [43] that magnetic monopoles accelerated by galactic magnetic fields could give rise to the highest energy cosmic rays (E 10¹⁹ eV) and explain the violation of the famous Greisen-Zatsepin-Kuzmin cut-off [44].

Also the condition c) does not represent a too serious problem for the survival of primordial magnetic fields. The time evolution law of a magnetic field in a conducting medium has been already written in Eq. (1.5).

Neglecting fluid velocity this equation reduces to the diffusion equation which implies that an initial magnetic configuration will decay away in a time

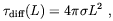
(1.17)

where L is the characteristic length scale of the spatial variation of B. In a cosmological framework, this means that a magnetic configuration with coherence length L₀ will survive until the present time t₀ (t = 0 corresponds to the big-bang time) only if _diff(L₀) > t₀. In our convention, L₀ corresponds to the present time length scale determined by the Hubble law

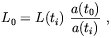
(1.18)

where a(t) is the Universe scale factor and L(t_i) is the length scale at the time at which the magnetic configuration was formed. Note that L₀ may not coincide with the actual size of the magnetic configuration since other effects (see below) may come-in to change the comoving coherence length. As we see from Eq. (1.17) the relevant quantity controlling the decay time of a magnetic configuration is the electric conductivity of the medium. This quantity changes in time depending on the varying population of the available charge carriers and on their kinetics energies. However, since most of the Universe evolution takes place in a matter dominated regime, during which all charge carriers are non-relativistic, our estimate of the magnetic diffusion length is simpler. In general, electric conductivity can be determined by comparing Ohm law J = E with the electric current density definition J = n e v, where for simplicity we considered a single charge carrier type with charge e, number density n and velocity v. The mean drift velocity in the presence of the electric field E is v ~ eE / m where m is the charge carrier mass and is the average time between particle collisions. Therefore the general expression for the electron conductivity is ⁽²⁾

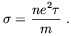
(1.19)

After recombination of electron and ions into stable atoms Universe conductivity is dominated by residual free electrons. Their relative abundance is roughly determined by the value that this quantity took at the time when the rate of the reaction p + e « H + became smaller than the Universe expansion rate. In agreement with the results reported in Ref. [46], we use

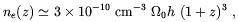
(1.20)

where ₀ is the present time density parameter and h is Hubble parameter. Electron resistivity is dominated by Thomson scattering off cosmic background photons. Therefore 1 / n _T, where _T = [(e⁴) / (6 m_e²)] is the Thomson cross section, and n = 4.2 × 10² (1 + z)³. Substituting these expressions in Eq. (1.19) we get

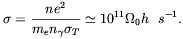
(1.21)

It is noticeable that after recombination time Universe conductivity is a constant. Finally, the cosmic diffusion length, i.e. the minimal size of a magnetic configuration which can survive diffusion during the Universe time-life t₀, is found by substituting t₀ = 2 × (₀ h²)^-1/2 s^-1 into Eq. (1.17) which, adopting ₀ = 1 and h = 0.6, gives

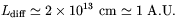
(1.22)

It follows from this result that magnetic diffusion is negligible on galactic and cosmological scales.

The high conductivity of the cosmic medium has other relevant consequences for the evolution of magnetic fields. Indeed, as we already mentioned in the Introduction, the magnetic flux through any loop moving with fluid is a conserved quantity in the limit . More precisely, it follows from the diffusion equation (1.5) and few vector algebra operations (see Ref. [15]) that

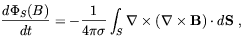
(1.23)

where S is any surface delimited by the loop. On scale where diffusion can be neglected the field is said to be frozen-in, in the sense that lines of force move together with the fluid. Assuming that the Universe expands isotropically ⁽³⁾, and no other effects come-in, magnetic flux conservation implies

(1.24)

This will be one of the most relevant equations in our review. It should be noted by the reader that B(t) represents the local strength of the magnetic field obtained by disregarding any effect that may be produced by spatial variations in its intensity and direction. Eq. (1.24) is only slightly modified in the case the a uniform magnetic field produce a significative anisotropic component in the Universe expansion (see Sec. 2.1).

Another quantity which is almost conserved due to the high conductivity of the cosmic medium is the, so-called, magnetic helicity, defined by

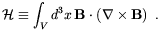
(1.25)

Helicity is closely analogous to vorticity in fluid dynamics. In a field theory language, H can be identified with the Chern-Simon number which is known to be related to the topological properties of the field. Indeed, it is known from Magnetohydrodynamics (MHD) that H is proportional to the sum of the number of links and twists of the magnetic field lines [47]. As it follows from Eq. (1.5), the time evolution of the magnetic helicity is determined by

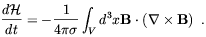
(1.26)

As we shall show in Chap. 4, several models proposed to explain the origin of primordial magnetic fields predict these fields to have some relevant amount of helicity.

In the previous section we have already mentioned the important role played by magnetic helicity in some MHD dynamo mechanisms driving an instability of small scale magnetic fields into large scale fields. A similar effect may take place at a cosmological level leading to significative corrections to the simple scaling laws expressed by the Eqs. (1.18, 1.24). Generally, these kind of MHD effects occur in the presence of some, turbulent motion of the conductive medium (note that Eqs. (1.18, 1.24) has been derived under the assumption of vanishing velocity of the fluid v = 0). Hydrodynamic turbulence is generally parameterized in terms of the Reynolds number, defined by

(1.27)

where is the kinematic viscosity. Fluid motion is said to be turbulent if Re >> 1. In the presence of a magnetic field another parameter turns-out to be quite useful. This is the magnetic Reynolds number defined by

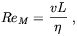
(1.28)

where = [1 / (4 )]. When Re_M >> 1 transport of the magnetic lines with the fluid dominates over diffusion. In this case hydrodynamic turbulence in a conducting medium give rise to magnetic turbulence. It is often assumed in MHD that a fully developed magnetic turbulence give rise to equipartion between the kinetic and the magnetic energy of the fluid. Whether equipartition hypothesis is valid or not is a controversial issue.

Both the hydrodynamic and magnetic Reynolds numbers can be very large in the early Universe. This is a consequence of the high electric conductivity and low viscosity of the medium and, especially, of the large scales which are involved. The electric conductivity of the early Universe has been computed by several authors. A first simple estimation of in the radiation dominated era was performed by Turner and Widrow [45]. In terms of the resistivity their result is ~ / T . A more exact series of calculations can be found in Ref. [48] which include logarithmic corrections due to Debye and dynamical screening. As a result a more correct expression for is

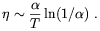
(1.29)

Other detailed computations of the Universe conductivity close to the QCD and the electroweak phase transitions are available in Refs. [49]. The kinematic viscosity follows the behavior [50]

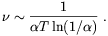
(1.30)

In the early Universe >> , i.e. Re_M >> Re. Concerning the absolute value of these parameters, using the previous expressions it is easy to verify that for a reasonable choice of the velocity field that may be produced by a phase transition, v 10^-3, both Re and Re_M are much larger than unity by several orders of magnitude, even for very small scales (for more details see Chap. 4). It seems that the early Universe was a quite "turbulent child" ! Turbulence is expected to cease after e⁺ e^- annihilation since this process reduces the plasma electron population and therefore increases the photon diffusion length hence also the kinematic viscosity. This should happen at a temperature around 1 MeV.

Turbulence is expected to produce substantial modification in the scaling laws of cosmological magnetic fields. This issue has been considered by several authors. Brandenburg, Enqvist and Olesen [51] first consider MHD in an expanding Universe in the presence of hydro-magnetic turbulence. MHD equations were written in a covariant form and solved numerically under some simplifying assumptions. The magnetic field was assumed to be distributed randomly either in two or three spatial dimensions. In the latter case a cascade (shell) model was used to reduce the number of degree of freedom. In both cases a transfer of magnetic energy from small to large magnetic configurations was observed in the simulations. In hydrodynamics this phenomenon is know as an inverse cascade. Cascade processes are know to be related to certain conservation properties that the basic equations obey [52]. In the two-dimensional inverse cascade, the relevant conserved quantity is the volume integral of the vector potential squared, d² x A², whereas in the three-dimensional cases it is the magnetic helicity. It was recently showed by Son [59] that no inverse cascade can develop in 3d if the mean value of H vanishes. If this is the case, i.e. in the presence of non-helical MHD turbulence, there is still an anomalous grow of the magnetic correlation length with respect to the scaling given in Eq. (1.18) but this is just an effect of a selective decay mechanism: modes with larger wavenumbers decay faster than those whose wavenumbers are smaller. Assuming Universe expansion is negligible with respect to the decay time, which is given by the eddy turnover time _L ~ L / v_L, and the decay of the large wavenumber modes does not affect those with smaller wavenumbers, Son found that the correlation length scale with time as

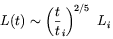
(1.31)

where _i = L_i / v_i is the eddy turnover time at t = 0. Assuming equipartition of the kinetic and magnetic energies, that is v_L ~ B_L, it follows that the energy decay with time like t^-6/5. When the Universe expansion becomes not negligible, i.e. when t > t₀, one has to take into account that the correlation length grows as ^2/5, where is the conformal time. Since ~ T^-1, it follows the T^-2/5 law. In the real situation, the final correlation length at the present epoch is,

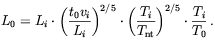
(1.32)

In the above, the first factor comes from the growth of the correlation length in the time interval 0 < t < t₀ when eddy decay is faster than Universe expansion; the second factor comes from the growth of L in the t > t₀ period; the last factor comes from trivial redshift due to the expansion of the Universe. T_nt is the temperature of the Universe when the fluid becomes non-turbulent. As we discussed T_nt ~ 1 MeV. If, for example, we assume that turbulence was produced at the electroweak phase transition, so that T_i = T_EW ~ 100 GeV, that v_i ~ 0.1 and L_i ~ 10^-2 r_H(T_EW) ~ 10^-2 cm, one find L₀ ~ 100 AU. This result has to be compared with the scale one would have if the only mechanism of dissipation of magnetic energy is resistive diffusion which, as we got in Eq. (1.22) is ~ 1 AU.

A larger coherence length can be obtained by accounting for the magnetic helicity which is probably produced during a primordial phase transition. The conservation of H has an important consequence for the evolution of the magnetic field. When H is non-vanishing, the short-scale modes are not simply washed out during the decay: their magnetic helicity must be transferred to the long-scale ones. Along with the magnetic helicity, some magnetic energy is also saved from turbulent decay. In other words, an inverse cascade is taking place. Assuming maximal helicity, i.e. that B · ( × B) ~ L B², the conservation of this quantity during the decay of turbulence implies the scaling law

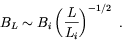
This corresponds to "line averaging", which gives a much larger amplitude of the magnetic field than the usual "volume averaging". Equipartition between magnetic and kinetic energy implies

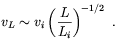
This relation together with the expression for the eddy decay time, _L = L / v_L, leads to the following scaling law for the correlation length of helical magnetic structures

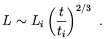
(1.33)

Comparing this result with Eq. (1.31), we see that in the helical case the correlation length grow faster than it does in the turbulent non-helical case. The complete expression for the scaling of L is finally obtained by including trivial redshift into Eq. (1.33). Since in the radiation dominated era T ^-1 ~ a ~ t^1/2, we have [50]

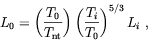
(1.34)

and

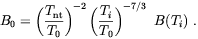
(1.35)

According to Son, [50] helical hydromagnetic turbulence survives longer than non-helical turbulence allowing T_nt to be as low as 100 eV. If again we assume that helical magnetic turbulence is generated at the electroweak phase transition (which will be justified in Chap. 4) we find

(1.36)

which is much larger than the result obtained in the non-helical case. It is worthwhile to observe that,as the scale derived in the previous expression is also considerably larger than the cosmological magnetic diffusion length scale given in Eq. (1.22), that magnetic field fields produced by the EW phase transition may indeed survive until present.

² In the case the average collision time of the charge carrier is larger than the Universe age _U, the latter has to be used in place of in Eq. 1.19 [45]. Back.

³ In the Sec. 2.1 we shall discuss under which hypothesis such an assumption is consistent with the presence of a cosmic magnetic field. Back.