2.1. The effect of a homogeneous magnetic field
It is well know from General Relativity that electromagnetic fields can affect the geometry of the Universe. The energy momentum tensor
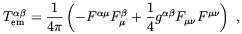
| (2.1) |
where
Fµ
is the electromagnetic field tensor, acts as a
source term in the Einstein equations. In the case of a
homogeneous magnetic field directed along the z-axis
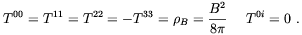
| (2.2) |
Clearly, the energy-momentum tensor becomes anisotropic due to the presence of the magnetic field. There is a positive pressure term along the x and y-axes but a "negative pressure" along the field direction. It is known that an isotropic positive pressure increases the deceleration of the universe expansion while a negative pressure tends to produce an acceleration. As a consequence, an anisotropic pressure must give rise to an anisotropy expansion law [53].
Cosmological models with a homogeneous magnetic field have been considered by several authors (see e.g. [54]). To discuss such models it is beyond the purposes of this review. Rather, we are more interested here in the possible signature that the peculiar properties of the space-time in the presence of a cosmic magnetic field may leave on the Cosmic Microwave Background Radiation (CMBR).
Following Zeldovich and Novikov [53] we shall consider the most general axially symmetric model with the metric
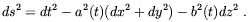
| (2.3) |
It is convenient to define
=
/ a;
=
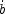/ b; and
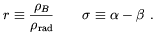
| (2.4) |
Then, assuming r,
< 1, the Einstein
equations are well approximated by
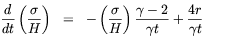
| (2.5) |
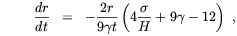
| (2.6) |
where H = (2 +
) and
are
defined by the equation of state p =
( - 1)
. It is easy to
infer from
the first of the previous equations that the magnetic field acts so as to
conserve the anisotropy that would otherwise decay with time
in the case r = 0. By substituting the asymptotic value of the
anisotropy, i.e.
6r,
into the evolution equation for r in the RD era
one finds
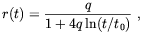
| (2.7) |
where q is a constant. Therefore, in the case the cosmic magnetic field is homogeneous, the ratio of the magnetic and blackbody radiation densities is not a constant, but falls logarithmically during the radiation era.
In order to determine the temperature anisotropy of the CMBR we assume that at the recombination time trec the temperature is everywhere Trec. Then, at the present time, t0, the temperature of relic photons coming from the x (or y) and z directions will be respectively
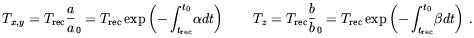
| (2.8) |
Consequently, the expected temperature anisotropy is
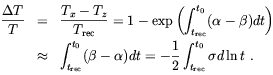
| (2.9) |
By using this expression, Zeldovich and Novikov estimated that a
cosmological magnetic field having today the strength of
10-9 ÷ 10-10 Gauss would produce a
temperature anisotropy
T / T
10-6.
The previous analysis has been recently updated by Barrow,
Ferreira and Silk [55].
In that work the authors derived an upper
limit on the strength of a homogeneous magnetic field at the recombination
time on the basis of the 4-year Cosmic Background Explorer (COBE)
microwave background isotropy measurements
[56]. As it is
well know COBE detected quadrupole anisotropies at a level
T / T ~
10-5 at an angular scale of few degrees.
By performing a suitable statistical average of the data and
assuming that the field keeps frozen-in since the recombination
till today, Barrow at al. obtained the limit
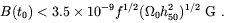
| (2.10) |
In the above f is a O(1) shape factor accounting for possible non-Gaussian characteristics of the COBE data set.
From this results we see that COBE data are not incompatible with a primordial origin of the galactic magnetic field even without invoking a dynamo amplification.