4.5. Magnetic fields from inflation

As noted by Turner and Widrow [45] inflation (for a comprehensive introduction to inflation see Ref. [46]) provides four important ingredients for the production of primeval magnetic fields.

• Inflation naturally produces effects on very large scales, larger than the Hubble horizon, starting from microphysical processes operating on a causally connected volume. If electromagnetic quantum fluctuations are amplified during inflation they could appear today as large-scale static magnetic fields (electric field should be screened by the high conductivity plasma).
• Inflation also provides the dynamical means to amplify these long-wavelength waves. If the conformal invariance of the electromagnetic field is broken in some way (see below) magnetic fields could be excited during the de Sitter Universe expansion. This phenomenon is analogous to particle production occurring in a rapidly changing space-time metric.
• During inflation (and perhaps during most of reheating) the Universe is not a good conductor so that magnetic flux is not conserved and the ratio r of the magnetic field with the radiation energy densities can increase.
• Classical fluctuations with wavelength H^-1 of massless, minimally coupled fields can grow super-adiabatically, i.e. their energy density decrease only as ~ a^-2 rather than a^-4.

The main obstacle on the way of this nice scenario is given by the fact that in a conformally flat metric, like the Robertson-Walker usually considered, the background gravitational field does not produce particles if the underlying theory is conformally invariant [192]. This is the case for photons since the classical electrodynamics is conformally invariant in the limit of vanishing fermion masses. Several ways out this obstacle have been proposed. Turner and Widrow [45] considered three possibilities. The first is to break explicitly conformal invariance by introducing a gravitational coupling, like R A_µ A^µ or R_µ A^µ A^µ, where R is the curvature scalar, R_µ is the Ricci tensor, and A^µ is the electromagnetic field. These terms breaks gauge invariance and give the photons an effective, time-dependent mass. In fact, one of the most severe constraints to this scenario come from the experimental upper limit to the photon mass, which today is m < 2 × 10^-16 eV [193]. Turner and Widrow showed that for some suitable (though theoretically unmotivated) choice of the parameters, such a mechanism may give rise to galactic magnetic fields even without invoking the galactic dynamo. We leave to the reader to judge if such a booty deserve the abandonment of the theoretical prejudice in favor of gauge invariance. A different model invoking a spontaneous breaking of gauge symmetry of electromagnetism, implying nonconservation of the electric charge, in the early stage of the evolution of the Universe has been proposed by Dolgov and Silk [194].

The breaking of the conformal invariance may also be produced by terms of the form R_µ F^µ F / m² or R F^µ F_µ, where m is some mass scale required by dimensional considerations. Such terms arise due to one-loop vacuum polarization effects in curved space-time, and they have the virtue of being gauge invariant. Unfortunately, Turner and Widrow showed that they may account only for a far too small contribution to primordial magnetic fields. The third way to break conformal invariance discussed by Turner and Widrow invoke a coupling of the photon to a charged field which is not conformally coupled or the anomalous coupling to a pseudoscalar. This mechanism was already illustrated in the previous section.

The anomaly can give rise to breaking of the conformal invariance also in a different way. The kind of anomaly we are now discussing about is the conformal anomaly, which is related to the triangle diagram connecting two photons to a graviton. It is known (for a review see Ref. [195]) that this kind of diagrams breaks conformal invariance by producing a nonvanishing trace of the energy-momentum tensor

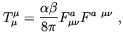
(4.77)

where is the fine-structure constant of the theory based on the SU(N) gauge-symmetry with N_f fermion families, and

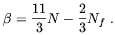
(4.78)

Dolgov [196] pointed-out that such an effect may lead to strong electromagnetic fields amplification during inflation. In fact, Maxwell equations are modified by the anomaly in the following way

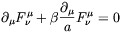
(4.79)

which, in the Fourier space, gives rise to the equation

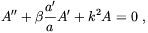
(4.80)

where A is the amplitude of the vector potential, and a prime stands for a derivation respect to the conformal time . At the inflationary stage, when a' / a = - 1 / Dolgov found a solution of (4.80) growing like (H / k)^/2. Since k^-1 grows well above the Hubble radius during the de Sitter phase, a huge amplification can be obtained if > 0. Dolgov showed that for ~ 1 the magnetic field generated during the inflationary stage can be large enough to give rise to the observed fields in galaxies even without a dynamo amplification. Unfortunately, such a large value of seems to be unrealistic ( 0.06 for SU(5) with three charged fermions). The conclusion is that galactic magnetic fields might be produced by this mechanism only invoking a group larger than SU(5) with a large number of fermion families, and certainly no without the help of dynamo amplification.

As we discussed in the above conformal invariance of the electromagnetic field is generally spoiled whenever the electromagnetic field is coupled to a scalar field. Ratra [197] suggested that a coupling of the form e F^µ F_µ, where is a arbitrary parameter, may lead to a huge amplification of electromagnetic quantum fluctuations into large scale magnetic fields during inflation. Such a coupling is produced in some peculiar models of inflation with an exponential inflaton potential [198]. It should be noted by the reader that the scalar field coincide here with the inflaton field. According to Ratra, present time intergalactic magnetic fields as large as 10^-9 G may be produced by this mechanism which would not require any dynamo amplification to account for the observed galactic fields. Unfortunately, depending on the parameter of the underling model, the predicted field could also be as low as 10^-65 G !

A slightly more predictive, and perhaps theoretically better motivated, model has been proposed independently by Lemoine and Lemoine [199] , and Gasperini, Giovannini and Veneziano [200], which is based on superstring cosmology [201]. This model is based on the consideration that in string theory the electromagnetic fields is coupled not only to the metric (g_µ), but also to the dilaton field . In the low energy limit of the theory, and after dimensional reduction from 10 to 4 space-time dimensions, such a coupling takes the form

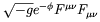
(4.81)

which breaks conformal invariance of the electromagnetic field and coincides with the coupling considered by Ratra [197] if = -1. Ratra, however, assumed inflation to be driven by the scalar field potential, which is not the case in string cosmology. In fact, typical dilaton potentials are much too steep to produce the required slow-roll of the inflaton (= dilaton) field. According to string cosmologists, this problem can be solved by assuming inflation to be driven by the kinetic part of the dilaton field, i.e. from ' [201]. In such a scenario the Universe evolves from a flat, cold, and weakly coupled ( = - ) initial unstable vacuum state toward a curved, dilaton-driven, strong coupling regime. During this period, called pre-big-bang phase, the scale factor and of the dilaton evolve as

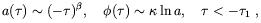
(4.82)

with > 1 and < 0. At > - ₁ it begins the standard FRW phase with a radiation dominated Universe. In the presence of the non-trivial dilaton background the modified Maxwell equations takes the form [199]

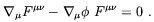
(4.83)

Electromagnetic field amplification from quantum fluctuations take place during the pre-big-bang phase when ' = / , where = . By following the evolution of the electromagnetic field modes from t = - to now, Lemoine and Lemoine estimated that, in the most simple model of dilaton-driven inflation (with V() = = p = 0) a very tiny magnetic field is predicted today

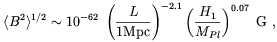
(4.84)

where H₁ = 1 / ₁, which is far too small to account for galactic fields.

Gasperini, Giovannini and Veneziano [200], reached a different conclusion, claiming that magnetic fields as large those required to explain galactic fields without dynamo amplification may be produced on the protogalactic scale. The reason for such a different result is that they assumed a new phase to exist between the dilaton-dominated phase and the FRW phase during which dilaton potential is nonvanishing. The new phase, called the string phase, should start when the string length scale _S becomes comparable to the horizon size at the conformal time _S [202]. Unfortunately, the duration of such a phase is quite unknown, which makes the model not very predictive.

Recently, several papers have been published (see e.g. Refs. [203, 204, 205]) which proposed the generation of magnetic fields by fluctuations of scalar (or pseudo-scalar) fields which were amplified during, or at the end, of inflation. Typically, all these models predict magnetic fields which need dynamo amplification to account for the observed galactic and cluster fields.