4.4. Magnetic helicity and electroweak baryogenesis

As we discussed in the introduction of our report, the cosmological magnetic flux is a nearly conserved quantity due to the high conductivity of the Universe. In this section we will focus on another quantity which, for the same reason, is approximatively conserved during most of the Universe evolution. This is the so called magnetic helicity defined by

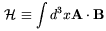
(4.60)

where A is the electromagnetic vector potential and B is the magnetic field. In the presence of a small value of the electric conductivity the time evolution of H is given by

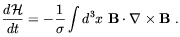
(4.61)

Besides for the fact to be a nearly conserved quantity, the magnetic helicity is a very interesting quantity for a number of different reasons. The main among these reasons are:

• In a field theory language H coincides with the Chern-Simon number which is know to be related to the topological properties of the gauge fields.
• Since H is a P (parity) and CP-odd function, the observation of a nonvanishing net value of this quantity would be a manifestation of a macroscopic violation of both these symmetries.
• It is know from magneto-hydro-dynamics that the presence of magnetic helicity can lead to the amplification of magnetic fields and contribute to their self-organization into a large scale ordered configuration (see Sec. 1.4). The same phenomenon could take place at a cosmological level.

In the last few years, several authors proposed mechanisms for the production of magnetic helicity in the early Universe starting from particle physics processes. Cornwall [174] suggested that magnetic helicity was initially stored in the Universe under the form of baryons (B) and leptons (L) numbers possibly generated by some GUT scale baryogenesis mechanism. He assumed that an order one fraction of the total classically conserved B+L charge was dissipated by anomalous processes at the EW scale and showed that a small fraction of this dissipated charge, of the order of n_B+L T^-3, may have been converted into a magnetic helicity of the order of

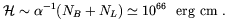
(4.62)

Another possibility is that before symmetry breaking of a non-Abelian gauge symmetry vacuum configurations existed which carried nonvanishing winding number. It was shown by Jackiw and Pi [175] that after symmetry breaking, one direction in isospin space is identified with electromagnetism, and the projection of the vacuum configuration becomes a magnetic field with non vanishing helicity.

A different mechanism was proposed by Joyce and Shaposhnikov [176]. In this case it was assumed that some excess of right-handed electrons over left-handed positrons was produced by some means (e.g. from some GUT scale leptogenesis) above a temperature T_R. At temperatures higher than T_R perturbative processes which changes electron chirality are out of thermal equilibrium (T_R ~ 3 TeV in the SM [177]). Therefore, a chemical potential for right electrons µ_R can be introduced above T_R. On the other hand, the corresponding charge is not conserved because of the Abelian anomaly, which gives

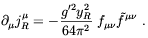
(4.63)

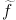In the above, f_µ and ^µ are, respectively, the U(1)_Y hypercharge field strength and its dual, g' is the associated gauge coupling constant, and y_R = - 2 is the hypercharge of the right electron. As it is well known, Eq. (4.63) relates the variation in the number of the right handed electrons N_R to the variation of the topological properties (Chern-Simon number) of the hypercharge field configuration. By rewriting this expression in terms of the hypermagnetic _Y and of the hyperelectric 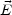_Y fields,

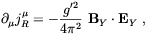
(4.64)

it is evident the relation of j_R^µ with the hypermagnetic helicity. It is worthwhile to observe that only the hypermagnetic helicity is coupled to the fermion number by the chiral anomaly whereas such a coupling is absent for the Maxwell magnetic helicity because of the vector-like coupling of the electromagnetic field to fermions. From Eq. (4.63) it follows that the variation in N_R, is related to the variation in the Chern-Simon number,

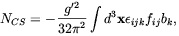
(4.65)

by N_R = 1/2 y_R² N_CS. In the above b_k represents the hypercharge field potential. The energy density sitting in right electrons is of order µ_R² T² and their number density of order µ_R T². Such fermionic number can be reprocessed into hypermagnetic helicity of order g'² kb², with energy of order k² b², where k is the momentum of the classical hypercharge field and b is its amplitude. Therefore, at b > T / g'² it is energetically convenient for the system to produce hypermagnetic helicity by "eating-up" fermions. It was showed by Joyce and Shaposhnikov [176], and in more detail by Giovannini and Shaposhnikov [178], that such a phenomenon corresponds to a magnetic dynamo instability. In fact, by adding the anomaly term to the Maxwell like equations for the hyperelectric and hypermagnetic fields these authors were able to write the anomalous magneto-hydrodynamical (AMHD) equations for the electroweak plasma in the expanding Universe, including the following generalized hypermagnetic diffusivity equation

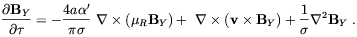
(4.66)

In the above a is the Universe scale factor, ' g'² / 4, = a^-1(t) dt is the conformal time, and the electric conductivity of the electroweak plasma [49]. By comparing Eq. (4.6615]) one sees that the first term on the r.h.s. of Eq. (4.66) corresponds to the so-called dynamo term which is know to be related to the vorticity in the plasma flux [11]. We see that the fermion asymmetry, by providing a macroscopic parity violation, plays a similar role of that played by the fluid vorticity in the dynamo amplification of magnetic fields. In the scenario advocated in Ref. [176, 178], however, it is not clear what are the seed fields from which the dynamo amplification start from. Clearly, no amplification takes place if the initial value of the hypermagnetic field vanishes. Perhaps, seeds field may have been provided by thermal fluctuations or from a previous phase transition although this is a matter of speculation. According to Joyce and Shaposhnikov [176], assuming that a large right electron asymmetry µ_R / T ~ 10^-2 was present when T = T_R, magnetic field of strength B ~ 10²² G may have survived until the EWPT time with typical inhomogeneity scales ~ 10⁶ / T.

Another interesting point raised by Giovannini and Shaposhnikov [178] is that the Abelian anomaly may also process a preexisting hypermagnetic helicity into fermions. In this sense the presence of tangled magnetic fields in the early Universe may provide a new leptogenesis scenario.

Indeed, assuming that a primordial hypermagnetic field _Y was present before the EWPT with some non-trivial topology (i.e. <B_Y · × B_Y> 0) the kinetic equation of right electrons for T > T_c is

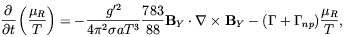
(4.67)

where

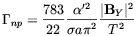
(4.68)

is the rate of the N_R nonconserving anomalous processes whereas is the rate of the perturbative ones. In the case _np > , as a consequence of Eq. (4.67), one finds

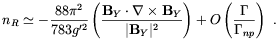
(4.69)

Below the critical temperature the hypermagnetic fields are converted into ordinary Maxwell magnetic fields. Similarly to the usual EW baryogenesis scenario, the fermion number asymmetry produced by the Abelian anomaly may survive the sphaleron wash-out only if the EWPT is strongly first order, which we know to be incompatible with the standard model in the absence of primordial magnetic fields. However, Giovannini and Shaposhinikov argued that this argument might not apply in the presence of strong magnetic fields (we shall discuss this issue in Chap. 5). If this is the case a baryon asymmetry compatible with the observations might have been generated at the EW scale. Another prediction of this scenario is the production of strong density fluctuations at the BBN time which may affect the primordial synthesis of light elements [179].

Primordial magnetic fields and the primordial magnetic helicity may also have been produced by the interaction of the hypercharge component of the electromagnetic field with a cosmic pseudoscalar field condensate which provides the required macroscopic parity violation. This idea was first sketched by Turner and Widrow [45] in the framework of an inflationary model of the Universe which we shall discuss in more details in the next section. Turner and Widrow assumed the pseudoscalar field to be the axion, a particle which existence is invoked for the solution of the strong CP problem (for a review see Ref. [180]). Although the axion is supposed to be electrically neutral it couples to electromagnetic field by means of the anomaly. Indeed, the effective Lagrangian for axion electrodynamics is

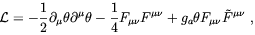
(4.70)

where g_a is a coupling constant of order , the vacuum angle = _a / f_a, _a is the axion field, f_a is the Peccei-Quinn symmetry breaking scale (see Ref. [180]), F_µ is the electromagnetic field strength and 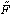^µ is its dual. Since the axion field, as any other scalar field, is not conformally invariant (see the next section), it will be amplified during the inflationary expansion of the Universe starting from quantum fluctuations, giving rise to <²> ~ (H₀ / f_a)², which can act as a source term for the electromagnetic field ⁽¹⁷⁾.

Carroll and Field [182] reconsider in more details the idea of Turner and Widrow and found that the evolution of a Fourier mode of the magnetic field with wave number k is governed by the equation

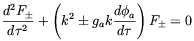
(4.71)

where F _± = a²(B_x ± iB_y) are the Fourier modes corresponding to different circular polarizations, and is the conformal time. One or both polarization modes will be unstable for k < g_a |d_a / d|, whereas both polarization modes can becomes unstable to exponential growth if is oscillating. In this case it seems as if a quite strong magnetic field could be produced during inflation. However, such a conclusion was recently criticized by Giovannini [183] who noted that above the EWPT temperature QCD sphalerons [184] are in thermal equilibrium which can effectively damp axion oscillations. In fact, because of the presence of QCD sphaleron the axion equation of motion becomes

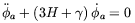
(4.72)

where [184]

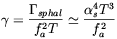
(4.73)

(where _s = g_s² / 4). Giovannini founds that sphaleron induced damping dominates over damping produced by the expansion of the Universe if f_a > 10⁹ GeV. Since astrophysical and cosmological bounds [125] leave open a window 10¹⁰ GeV < f_a < 10¹² GeV, it follows that no magnetic fields amplification was possible until QCD sphaleron went out of thermal equilibrium. A very tiny magnetic helicity production from axion oscillations may occur at lower temperatures. In fact, Giovannini [183] estimated that in the temperature range 1 GeV > T > 10MeV a magnetic helicity of the order of

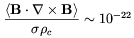
(4.74)

may be generated, which is probably too small to have any phenomenological relevance.

Generation of magnetic fields from coherent oscillations or roll-down of pseudoscalar fields different from the axion has been also considered in the literature. It is interesting that pseudoscalar fields with an axion-like anomalous coupling to the electromagnetic field appear in several possible extension of the SM. Typically these fields have only perturbative derivative interactions and therefore vanishing potential at high temperatures, and acquire a potential at lower temperatures through non-perturbative interactions. The generic form of this potential is V() = V₀⁴ A(/f), where A is a bounded function of the "Peccei-Quinn" scale f which in this case can be as large as the Planck scale. The pseudoscalar mass m ~ V₀² / f may range from a few eV to 10¹² GeV. The amplification of magnetic fields proceeds in a way quite similar to that discussed for axions. The evolution equation of the electromagnetic Fourier modes were derived by Brustein and Oaknin [185] who added to Eq. (4.71) the effect of a finite electric conductivity, finding

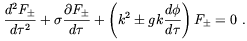
(4.75)

If the pseudoscalar field is oscillating, the field velocity d / d changes sign periodically and both polarization modes are amplified, each during a different semi-cycle. Each mode is amplified during one part of the cycle and damped during the other part of the cycle. Net amplification results when g kd / d > ² and the total amplification is exponential in the number of cycles. Taking into account that ~ 10T before the EWPT [49], Brustein and Oaknin found that a huge amplification can be obtained from pseudoscalar field oscillations at T ~ 1 TeV, for a scalar mass m of few TeV and g f ~ 10. This is a particularly interesting range of parameters as in this case the pseudoscalar field dynamics could be associated with breaking of supersymmetry at the TeV scale. Since only a limited range of Fourier modes are amplified, with k not too different from T, and modes with k / T < _EW << 1 are rapidly dissipated, amplified fields may survive until the EWPT only if amplification occurred just before the transition. If this is a natural assumption may be a matter of discussion. However, it was pointed-out by Brustein and Oaknin [185] that if, depending on the form of the pseudoscalar field potential, this field rolls instead of oscillating, then the hypermagnetic fields would survive until EWPT even if the amplification takes place at higher temperatures before the transition. In this case there could be interesting consequences for the EW baryogenesis. This is so, because the pseudoscalar field may carry a considerable amount of helicity. According to what discussed in the above, this number will be released in the form of fermions and baryons if the EWPT is strongly first order. Brustein and Oaknin argued that this mechanism could naturally generate the observed BAU.

Clearly, a more serious problem of this mechanism is the same of other EW baryogenesis scenarios, namely to have a strongly first order EWPT. An interesting possibility which was proposed by two different groups [178, 186] is that strong magnetic fields may enhance the strength of the EWPT (see Chap. 5). Unfortunately, detailed lattice computations [187] showed that this is not the case. Furthermore, in a recent work by Comelli et al. [188] it was shown that strong magnetic fields also increase the rate of EW sphalerons so that the preservation of the baryon asymmetry calls for a much stronger phase transition than required in the absence of a magnetic field. The authors of Ref. [188] showed that this effect overwhelms the gain in the phase transition strength (see Sec. 5.3.2). Therefore, the only way for the kind of EW baryogenesis mechanism discussed in the above to work is to invoke for extensions of the standard model which allow for a strong first order EWPT [144].

Electroweak strings, which we introduced in the previous section, may also carry a net hypermagnetic helicity and act as a source of the observed BAU. One of the interesting features of this objects is that they should have been formed during the EWPT even if this transition is second order or just a cross over [173]. It is known that electroweak strings can carry magnetic helicity, hence a baryon number, which is related to the twisting and linking of the string gauge fields [159, 189]. Several authors (see e.g. Ref. [190]) tried to construct a viable EW baryogenesis scenario based on these embedded defects. Many of these models, however, run into the same problems of more conventional EW baryogenesis scenarios. An interesting attempt was done by Barriola [191] who invoked the presence of a primordial magnetic field at the EWPT time. Barriola observed that the production and the following decay of electroweak strings give rise, in the presence of an external magnetic field, to a variation in the baryon number B in the time interval dt, given by

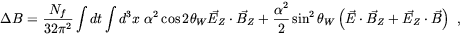
(4.76)

where 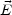_Z and _Z are the Z-electric and Z-magnetic fields of the strings whereas 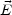and are the corresponding standard Maxwell fields. The first term in the r.h.s. of (4.76) represents the change in the helicity of the string network, and the second and third terms come form the coupling of the string fields with the external Maxwell fields. Whereas, the first term averages to zero over a large number of strings, the other terms may not. Clearly, some bias is required to select a direction in the baryon number violation. In the specific model considered by Barriola this is obtained by a CP violation coming from the extension of the Higgs sector of the SM, and from the dynamics of strings which are supposed to collapse along their axis. It was concluded by Barriola that such a mechanism could account for the BAU. Unfortunately, it is quite unclear if the invoked out-of-equilibrium mechanism based on the string collapse could indeed be effective enough to avoid the sphaleron wash-out. We think, however, that this possibility deserves further study.

¹⁷ The careful reader may wonder what is the fate of axions in the presence of cosmic magnetic fields. Interestingly, it was showed by Ahonen, Enqvist and Raffelt [181] that although oscillating cosmic axions drives an oscillating electric field, the ensuing dissipation of axions is found to be inversely proportional to the plasma conductivity and is, therefore, negligible. Back.