5.1.3. Electrons in an External Field

We might be tempted to use, for the electron, the formalism used for the proton with the Landé factor replaced by g_e = 2 + / . However as we shall see for magnetic fields sufficiently strong as to make the proton heavier than the neutron the change in energy of the electron would appear to be larger than the mass of the electron itself. The point particle formalism breaks down and we have solve QED, to one loop, in a strong magnetic field; fortunately this problem was treated by Schwinger [37]. The energy of an electron with p_z = 0, spin up and in the lowest Landau level is

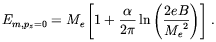
(5.16)

For field strengths of subsequent interest this correction is negligible; the energy of an electron in the lowest Landau level, with spin down and a momentum of p_z is

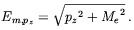
(5.17)

and with wave function similar to those of the proton

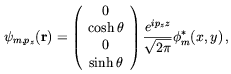
(5.18)

where the boost rapidity, 2, is defined below Eq. (5.7) while the Landau level wave function is defined in Eq. (5.5). The reason the complex conjugate wave function appears is that the electron charge is opposite to that of the proton.