5.1.4. Effects of Magnetic Fields on Strong Forces

We must be sure that shifts due to changes of color strong forces will not shift states in the opposite direction. The best method to study masses of QCD bound states is the use of sum rules [218]. This method uses the SVZ [219] generalized short distance expansion that includes not only perturbative pieces, but also higher dimensional operators like the chiral and gluon condensates reflecting the non Abelian nature of the vacuum. Fortunately the proton has a simple structure [218] which reflects the fact that if chiral symmetry is restored the proton and neutron masses vanish.

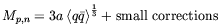
(5.19)

where a is a constant. Meson mass terms are more involved; for example the mass is

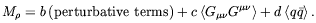
(5.20)

b, c and d are constants of comparable magnitude [218]. As we shall show it is only the change of <q 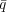> due to external magnetic fields that may be obtained in a reliable manner.

In the presence of external fields we expect the chiral condensates for quarks of different charges to vary and Eq. (5.19) becomes

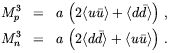
(5.21)

To first order in condensate changes we find

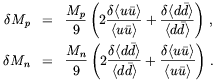
(5.22)

Combining

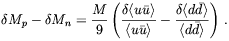
(5.23)

A simple method for studying the behavior of the chiral condensates in the presence of external constant fields is through the use of the Nambu-Jona-Lasinio model [220]. This has been done by Klevansky and Lemmer [221] and a fit to their results is

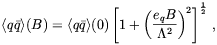
(5.24)

with = 270 MeV and e_q the charge on the quark. To lowest order we find

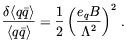
(5.25)

and

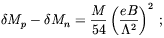
(5.26)

As in the previous section, these corrections are such as drive the proton energy up faster than that of the neutron. One can understand the sign of this effect; the radius of a quark-antiquark pair will decrease with increasing magnetic field thus making the condensate larger. As the u quark has twice the charge of the d quark, its condensate will grow faster and as there are more u quarks in the proton than in the neutron its mass will increase faster.

The fact that our estimate of the sign of the neutron-proton mass difference is the same as that due to electromagnetic effects is crucial. QCD sum rules and our method of evaluating the chiral condensates are both crude and the magnitude of the mass difference is uncertain. Had the sign of the hadronic correction been opposite, cancellations could have occurred and the argument for a narrowing of the mass difference and ultimate reversal could not have been made. We are quite sure of the sign of the chiral change. The magnetic field acts in the naive way in the spin of the scalar bound state in the condensate so it is sure that goes as calculated [222].