Magnetic Fields in the Early Universe - D. Grasso and H.R. Rubinstein

5.1.5. Proton Life Time

First we study the decay kinematics.

Combining Eq. (5.3), Eq. (5.14) and Eq. (5.26) we find the proton-neutron energy difference as a function of the applied magnetic field,

(5.27)

B₁₄ is the strength of the magnetic field in units of 10¹⁴ T (1 T = 10⁴ G). The neutron becomes stable for B > 1.5 × 10¹⁴ T and the proton becomes unstable to beta

decay for B > 2.7 × 10¹⁴ T. We shall now turn to a calculation of the life time of the proton for fields satisfying the last inequality.

With the wave functions of the various particles in the magnetic fields we may define field operators for these particles. For the proton and electron we shall restrict the summation over states to the lowest Landau levels with spin up, down respectively; for magnetic fields of interest the other states will not contribute to the calculation of decay properties. For the same reason, the neutron field will be restricted to spin down only. The proton and neutron kinematics will be taken as non-relativistic.

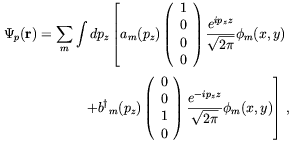
(5.28)

with phi _m(x, y) defined in Eq. (5.5) and the energy, E_m(p_z) in Eq. (5.8). a_m(p_z) is the annihilation operator for a proton with momentum p_zz and angular momentum m; b_m(p_z) is the same for the negative energy states. For the neutron the field is

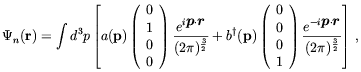
(5.29)

with an obvious definition of the annihilation operators. For the electron we use fully relativistic kinematics and the field is

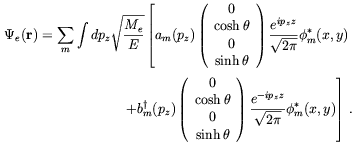
(5.30)