5.2. Screening of Very Intense Magnetic Fields by chiral symmetry breaking

Now we discuss another interesting phenomenon if very strong fields could be created.

In very intense magnetic fields, B > 1.5 × 10¹⁸ G, the breaking of the strong interaction SU(2) × SU(2) symmetry arranges itself so that instead of the neutral field acquiring a vacuum expectation value it is the charged field that does and the magnetic field is screened.

In the previous section we discussed that fields with complicated interactions of non-electromagnetic origin can induce various instabilities in the presence of very intense magnetic fields. By very intense we mean 10¹⁸ G to 10²⁴ G. Fields with anomalous magnetic moments [223] or fields coupled by transition moments [216] may induce vacuum instabilities. The usual breaking of the strong interactions, chiral symmetry (SM), is incompatible with very intense magnetic fields. Using the standard SU(2) × SU(2) chiral model we show that magnetic fields B B_c with B_c = sqrt[2] m f are screened; f = 132 MeV is the pion decay constant and m is the mass of the charged pions. This result is opposite to what occurs in a superconductor; in that case it is weak fields that are screened and large ones penetrate and destroy the superconducting state.

As the magnetic fields are going to be screened we must be very careful in how we specify an external field. One way would be to give f a spatial dependence and take it to vanish outside some large region of space. In the region that f vanishes we could specify the external field and see how it behaves in that part of space where chiral symmetry is broken. This is the procedure used in studying the behavior of fields inside superconductors. In the present situation we find this division artificial and, instead of specifying the magnetic fields, we shall specify the external currents. Specifically we will look, at first, at the electromagnetic field coupled to the charged part of the model and to the current I in a long straight wire. From this result it will be easy to deduce the behavior in other current configurations. We will discuss a solenoidal current configuration towards the end of this work.

The Hamiltonian density for this problem is

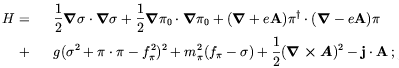
(5.39)

j is the external current. We have used cylindrical coordinates with the two dimensional vector normal to the z direction. We will study this problem in the limit of very large g, where the radial degree of freedom of the chiral field is frozen out and we may write

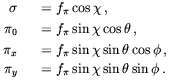
(5.40)

In terms of these variables the Hamiltonian density becomes

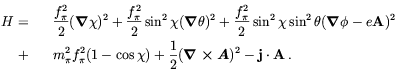
(5.41)

The angular field can be eliminated by a gauge transformation. For a current along a long wire we have

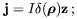
(5.42)

The vector potential will point along the z direction, A = Az and the fields will depend on the radial coordinate only. The equations of motion become

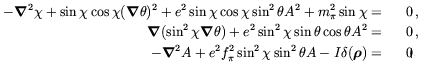
(5.43)

In the absence of the chiral field the last of the Eqs. (5.43) gives the classical vector potential due to a long wire

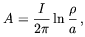
(5.44)

with a an ultraviolet cutoff. The energy per unit length in the z direction associated with this configuration is

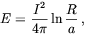
(5.45)

where R is the transverse extent of space (an infrared cutoff).

Before discussing the solutions of (5.43) it is instructive to look at the case where there is no explicit chiral symmetry breaking, m = 0. The solution that eliminates the infrared divergence in Eq. (5.45) is = = / 2 and A satisfying

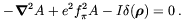
(5.46)

For any current the field A is damped for distances > 1 / ef and there is no infrared divergence in the energy. (Aside from the fact that chiral symmetry is broken explicitly, the reason the above discussion is only of pedagogical value is that the coupling of the pions to the quantized electromagnetic field does break the SU(2) × SU(2) symmetry into SU(2) × U(1) and the charged pions get a light mass, m ~ 35 MeV [193], even in the otherwise chiral symmetry limit.)

The term in Eq. (5.41) responsible for the pion mass prevents us from setting = / 2 everywhere; the energy density would behave as f² m² R², an infrared divergence worse than that due to the wire with no chiral field present. We expect that will vary from / 2 to 0 as increases and that asymptotically we will recover classical electrodynamics. Although we cannot obtain a closed solution to Eqs. (5.43), if the transition between = / 2 and = 0 occurs at large , we can find an approximate solution. The approximation consists of neglecting the ( )² term in Eq. (5.41); we shall return to this shortly. The solution of these approximate equations of motion is

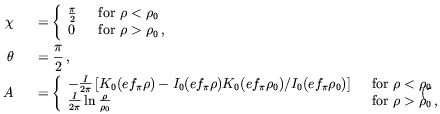
(5.47)

₀ is a parameter to be determined by minimizing the energy density of Eq. (5.41). Note that for > ₀ the vector potential as well as the field return to values these would have in the absence of any chiral fields and that for < ₀ the magnetic field decreases exponentially as B ~ exp(-ef ). The physical picture is that, as in a superconductor, near = 0 a cylindrical current sheet is set up that opposes the current in the wire and there is a return current near = ₀; Ampère's law insures that the field at large distances is as discussed above. The energy density for the above configuration, neglecting the spatial variation of , is

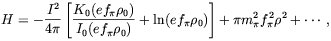
(5.48)

where the dots represent infrared and ultraviolet regulated terms which are, however, independent of ₀. For ₀ > 1 / ef the term involving the Bessel functions may be neglected and minimizing the rest with respect to ₀ yields

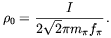
(5.49)

This is the main result of this work.

We still have to discuss the validity of the two approximations we have made. The neglect of the Bessel functions in Eq. (5.48) is valid for ef ₀ > 1 which in turn provides a condition on the current I, eI / m > 2 sqrt[2] or more generally

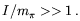
(5.50)

The same condition permits us to neglect the spatial variation of around = ₀. Let vary from / 2 to 0 in the region - d/2 to + d/2, with 1 / d of the order of f or m. The contribution of the variation of to the energy density is H = ³ f² ₀ d. Eq. (5.50) insures that H is smaller than the other terms in Eq. (5.48).

Eq.(5.49) has a very straightforward explanation. It results from a competition of the magnetic energy density 1 / 2 B² and the energy density of the pion mass term m² f²(1 - cos). The magnetic field due to the current I is B = I / 2 and the transition occurs at B = B_c, with B_c = [sqrt2]m f. The reader may worry that the magnetic fields very close to such thin wires are so large as to invalidate completely the use of the chiral model as a low energy effective QCD theory. In order to avoid this problem we may consider the field due to a solenoid of radius R. The field is zero outside the solenoid, B = B() z inside with B(R)=B₀. At no point does the field become unboundedly large. Using the same approximations as previously we obtain the following solutions of the equations of motion (for B₀ B_c)

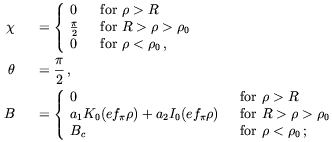
(5.51)

Continuity of the vector potential determines the coefficients a₁ and a₂,

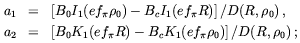
(5.52)

D(R, ₀) = K₁(e f R) I₁(e f ₀) - K₁(e f ₀) I₁(e f R) and ₀ is determined, once more, by minimizing the energy. For (R, ₀) > 1/e f

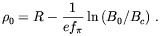
(5.53)

For B₀ B_c, = 0 everywhere and B() = B₀ in the interior of the solenoid. Thus, for any current configuration, the chiral fields will adjust themselves to screen out fields larger than B_c. Topological excitations may occur in the form of magnetic vortices; the angular field of Eq. (5.40) will wind around a quantized flux tube of radius 1 / e f [171].