5.3. The effect of strong magnetic fields on the electroweak vacuum

It was pointed out by Ambj orn and Olesen [223] (see also Ref.[225]) that the Weinberg-Salam model of electroweak interactions shows an instability at B 10²⁴ Gauss. The nature of such instability can be understood by looking at the expression of the energy of a particle with electric charge e, and spin s, moving in homogeneous magnetic field B directed along the z-axis. As we already discussed in Sec. 3.1, above a critical field B_c = m² / e particle energy is discretized into Landau levels

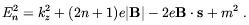
(5.54)

We observe that energy of scalar (s = 0) and spinor (s_z = ± 1/2) is always positive, and indeed no instability arise in QED (it is possible to verify that quantum one-loop corrections do not spoil this conclusion). In the case of vector particles (s_z = 0, ± 1), however, the lowest energy level (n = 0, k_z = 0, s_z = +1) becomes imaginary for B > B_c, which could be the signal of vacuum instability. The persistence of imaginary values of the one loop corrected lowest level energy [223] seems to confirm the physical reality of the instability.

As it is well known the Weinberg-Salam model contains some charged vector fields, namely the W^± gauge bosons. The coupling of the W_µ field to an external electromagnetic field A^ext_µ is given by

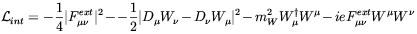
(5.55)

with

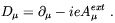
(5.56)

The important term in the previous expression is the "anomalous" magnetic moment term ie F^ext_µ W^µ W, which arises because the non-Abelian nature of the SU(2) component of the Weinberg-Salam model gauge group structure. Due to this term the mass eigenvalues of the W Lagrangian becomes

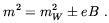
(5.57)

As expected from the considerations in the above, a tachyonic mode appears for B > B_c. The corresponding eigenvector for zero kinetic energy is determined by solving the equation of motions

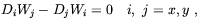
(5.58)

where W_1,2 = W_x ± iW_y. Ambjorn and Olesen argued that a suitable solution of this equation is

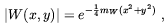
(5.59)

corresponding to a vortex configuration where W-fields wind around the z-axis. This configuration corresponds to the Nielsen-Olesen vortex solution [157]. A similar phenomenon should also take place for Z bosons. Given the linearity of the equations of motion it is natural to assume that a superpositions of vortices is formed above the critical field. This effect resemble the behaviour of a type-II superconductor in the presence of a critical field magnetic field. In that case U(1) symmetry is locally broken by the formations of a lattice of Abrikosov vortices in the Cooper-pairs condensate through which the magnetic field can flow. In the electroweak case this situation is reversed, with the formation of a W condensate along the vortices. Concerning the back-reaction of the W condensate on the magnetic field, an interesting effect arises. By writing the electric current induced by the W fields

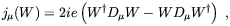
(5.60)

Ambj orn and Olesen noticed that its sign is opposite to the current induced by the Cooper pairs in a type-II superconductor, which is responsible for the Meissner magnetic field screening effect. Therefore, they concluded that the W-condensate induce anti-screening of the external magnetic field.

Although the Higgs field does not couple directly to the electromagnetic field (this is different from the case of a superconductor where the Cooper-pairs condensate couples directly to A^ext_µ), it does through the action of the W condensate. This can be seen by considering the Higgs, W potential in the presence of the magnetic fields:

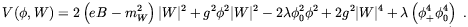
(5.61)

In the above ₀ and ₊ are respectively the Higgs field vev and charged component, g is the SU(2) coupling constant, and is the Higgs the self-interaction coupling constant. We see that the W-condensate influences the the Higgs field at classical level due to the ² |W |² term. It is straightforward to verify that if eB < m_W² = 1/2 g² ₀² the minimum of V(, W) sits in the standard field value = ₀ with no W condensate. Otherwise a W condensate is energetically favoured with the minimum of the potential sitting in

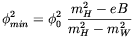
(5.62)

where

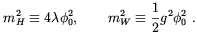
(5.63)

We see that the Higgs expectation value will vanish as the average magnetic field strength approaches zero, provided the Higgs mass is larger than the W mass. This seems to suggest that a W-condensate should exist for

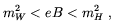
(5.64)

and that the SU(2) × U_Y(1) symmetry is restored above H⁽²⁾_c m_H²/e. Thus, anti-screening should produce restoration of the electroweak symmetry in the core of W vortices. If m_H < m_W the electroweak vacuum is expected to behave like a type I superconductor with the formation of homogeneous W-condensate above the critical magnetic field. The previous qualitative conclusion have been confirmed by analytical and numerical computations performed for m_H = m_W in Ref. [223], and for arbitrary Higgs mass in Refs. [226, 227].

A different scenario seems, however, to arise if thermal corrections are taken into account. Indeed, recent finite temperature lattice computations [187] showed no evidence of the Ambjorn and Olesen phase. According to Skalozub and Demchik [228] such a behaviour may be explained by properly accounting the contribution of Higgs and gauge bosons daisy diagrams to the effective finite temperature potential.

In conclusion, it is quite uncertain if the Ambj orn and Olesen phenomenon was really possible in the early Universe.