5.3.2. Sphalerons in strong magnetic fields

The sphaleron, is a static and unstable solution of the field equations of the electroweak model, corresponding to the top of the energy barrier between two topologically distinct vacua [230]. In the limit of vanishing Weinberg angle, _w 0, the sphaleron is a spherically symmetric, hedgehog-like configuration of SU(2) gauge and Higgs fields. No direct coupling of the sphaleron to a magnetic field is present in this case. As _w is turned on, the U_Y(1) field is excited and the spherical symmetry is reduced to an axial symmetry. A very good approximation to the exact solution is obtained using the Ansatz by Klinkhamer and Laterveer [231], which requires four scalar functions of r only,

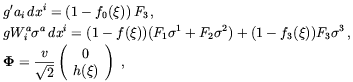
(5.72)

where g and g' are the SU(2)_L and U(1)_Y gauge couplings, v is the Higgs VEV such that M_W = g v / 2, M_h = sqrt[2 ] v, = gvr, ^a (a = 1, 2, 3) are the Pauli matrices, and the F_a's are 1-forms defined in Ref. [230]. The boundary conditions for the four scalar functions are

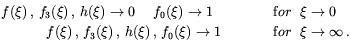
(5.73)

It is known [230, 231] that for _w 0 the sphaleron has some interesting electromagnetic properties. In fact, differently from the pure SU(2) case, in the physical case a nonvanishing hypercharge current J_i comes-in. At the first order in _w, J_i takes the form

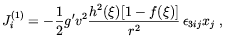
(5.74)

where h and f are the solutions in the _w 0 limit, giving for the dipole moment

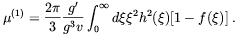
(5.75)

The reader should note that the dipole moment is a true electromagnetic one because in the broken phase only the electromagnetic component of the hypercharge field survives at long distances.

Comelli et al. [188] considered what happens to the sphaleron when an external hypercharge magnetic field, B_Y^ext, is turned on. They found that the energy functional is modified as

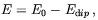
(5.76)

with

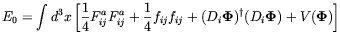
(5.77)

and

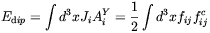
(5.78)

with f_{ij i} A^Y_j - _j A^Y_i. A constant external hypermagnetic field B^ext_Y directed along the x₃ axis was assumed. In the _w 0 limit the sphaleron has no hypercharge contribution and then E_dip⁽⁰⁾ = 0 . At O(_w), using (5.74) and (5.75) the authors of Ref. [188] got a simple magnetic dipole interaction energy

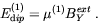
(5.79)

In order to assess the range of validity of the approximation (5.79) one needs to go beyond the leading order in _w and look for a nonlinear B^ext_Y-dependence of E. This requires to solve the full set of equations of motion for the gauge fields and the Higgs in the presence of the external magnetic field. Fortunately, a uniform B^ext_Y does not spoil the axial symmetry of the problem. Furthermore, the equation of motion are left unchanged (_i f^ext_ij = 0) with respect to the free field case. The only modification induced by B^ext_Y resides in the boundary conditions since - as - we now have

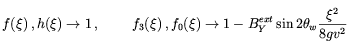
(5.80)

whereas the boundary condition for 0 are left unchanged.

The solution of the sphaleron equation of motions with the boundary conditions in the above were determined numerically by the authors of Ref. [188]. They showed that in the considered B^ext_Y-range the corrections to the linear approximation

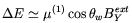
are less than 5%. For larger values of B^ext_Y non-linear effects increase sharply. However, as we discussed in the previous sections, for such large magnetic fields the broken phase of the SM is believed to become unstable to the formation either of W-condensates [223] or of a mixed phase [187]. In such situations the sphaleron solution does not exist any more. Therefore, it is safe to limit the previous analysis to values B^ext_Y 0.4 T2.

The reduction of sphaleron energy due to the interaction with the field Bc_Y has relevant consequences on the sphaleronic transition rate which is increased with respect to free field case. As a consequence, in an external magnetic field the relation between the Higgs VEV and the sphaleron energy is altered and Eq. (5.70) does not imply (5.69) any more. We can understand it by considering the linear approximation to E,

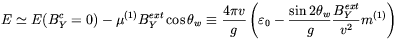
(5.81)

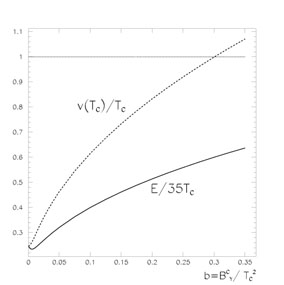
where m⁽¹⁾ is the O(_W) dipole moment expressed in units of e / _W M_W(T). From the Fig. 5.1 we see that even if v(T_c) / T_c 1 the washout condition E / T_c 35 is far from being fulfilled.

Figure 5.1. The VEV at the critical temperature, v(Tc), and the sphaleron energy vs. the external magnetic field for Mh = MW. We see that even if v(Tc) / Tc 1 the washout condition E / Tc 35 is far from being fulfilled. From Ref. [188].

It follows form the previous considerations, that even if a strong magnetic fields might increase the strength of the EWPT, such an effect would not help baryogenesis.