5.3.1. The electroweak phase transition in a magnetic field

We shall now consider the possible effects of strong magnetic fields on the electroweak phase transition (EWPT). As it is well known, the properties of the EWPT are determined by the Higgs field effective potential. In the framework of the minimal standard model (MSM), taking into account radiative corrections from all the known particles and for finite temperature effects, one obtains that

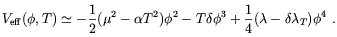
(5.65)

where is the radial component of the Higgs field and T is the temperature (for the definitions of the coefficients see e.g. Ref. [186]).

A strong hypermagnetic field can produce corrections to the effective potential as it affects the charge particles propagators (see below). There is, however, a more direct and simpler effect of magnetic and hypermagnetic fields on the EWPT which was recently pointed-out by Giovannini and Shaposhnikov [178] and by Elmfors, Enqvist and Kainulainen [186]. The authors of Refs. [178, 186] noticed that hypermagnetic fields affect the Gibbs free energy (in practice the pressure) difference between the broken and the unbroken phase, hence the strength of the transition. The effect can be understood by the analogy with the Meissner effect, i.e. the expulsion of the magnetic field from superconductors as consequence of photon getting an effective mass inside the specimen. In our case, it is the Z-component of the hypercharge U(1)_Y magnetic field which is expelled from the broken phase. This is just because Z-bosons are massive in that phase. Such a process has a cost in terms of free energy. Since in the broken phase the hypercharge field decomposes into

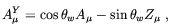
(5.66)

we see that the Gibbs free energy in the broken and unbroken phases are

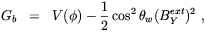
	(5.67)
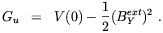
	(5.68)

where B^ext_Y is the external hypermagnetic field. In other words, compared to the case in which no magnetic field is present, the energy barrier between unbroken and broken phase, hence the strength of the transition, is enhanced by the quantity 1/2 sin² _w (B^ext_Y)². According to the authors of Refs. [178, 186] this effect can have important consequence for baryogenesis.

In any scenario of baryogenesis it is crucial to know at which epoch do the sphaleronic transitions, which violate the sum (B + L) of the baryon and lepton numbers, fall out of thermal equilibrium. Generally this happens at temperatures below 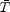such that

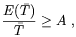
(5.69)

where E(T) is the sphaleron energy at the temperature T and A 35 - 45 , depending on the poorly known prefactor of the sphaleron rate. In the case of baryogenesis at the electroweak scale one requires the sphalerons to drop out of thermal equilibrium soon after the electroweak phase transition. It follows that the requirement 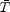= T_c, where T_c is the critical temperature, turns eq. (5.69) into a lower bound on the Higgs vacuum expectation value (VEV),

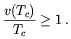
(5.70)

As we already discussed, it is by now agreed [143] that the standard model (SM) does not have a phase transition strong enough as to fulfill Eq. (5.70), whereas there is still some room left in the parameter space of the minimal supersymmetric standard model (MSSM) [144].

The interesting observation made in Refs. [178, 186] is that a magnetic field for the hypercharge U(1)_Y present for T > T_c may help to fulfill Eq. (5.70). In fact, it follows from the Eqs. (5.67), that in presence of the magnetic field the critical temperature is defined by the expression

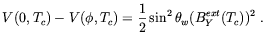
(5.71)

This expression implies a smaller value of T_c than that it would take in the absence of the magnetic field, hence a larger value of the ratio (5.70).

Two major problems, however, bar the way of this intriguing scenario. The first problem is that by affecting fermion, Higgs and gauge field propagators, the hypermagnetic field changes the electroweak effective potential in a nontrivial way. Two different approaches have been used to estimate the relevance of this kind of effects based either on lattice simulations [143] or analytical computations [228]. Both approaches agreed in the conclusion that for a Higgs field mass compatible with the experimental constraints (m_H > 75 GeV), and for field strengths B, B_Y 10²³ G, the standard model EWPT is second order or a cross-over. Although this negative result could, perhaps, be overcome by adopting a supersymmetrical extension of the standard model (see e.g. Ref. [144]), a second, and more serious problem arises by considering the effect of the magnetic field on the anomalous processes (sphalerons) which are responsible for lepton and baryon violation at the weak scale. This effect will be the subject of the next section.