


1.3. The Cosmological Constant

The cosmological constant has been recently reviewed by
Peebles (1988)
and by Weinberg (1989).
(See also
Klapdor and Grotz, 1986).
The wealth cosmological models that can arise through simply introducing
 is
discussed in the great ancient book by
Tolman (1934).
is
discussed in the great ancient book by
Tolman (1934).
Einstein presented a version of his famous field equations containing
an additional constant of nature, the Cosmological Constant,
 . The
consequence of introducing this ad hoc term into the equations can be
seen by studying the dynamical equations with the
. The
consequence of introducing this ad hoc term into the equations can be
seen by studying the dynamical equations with the
 -term. In the
simplest case of zero pressure (which approximates the present day
circumstances):
-term. In the
simplest case of zero pressure (which approximates the present day
circumstances):
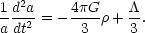
| (14) |
This is the generalization of (5, 6, 7).
A positive  -term
increases the acceleration of the expansion, and
gives rise to the possibility that the two terms on the right hand
side of (14) can at some time during the evolution balance:
-term
increases the acceleration of the expansion, and
gives rise to the possibility that the two terms on the right hand
side of (14) can at some time during the evolution balance:
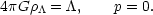
|
This "zero-acceleration" time can easily be shown to occur at a
redshift
z given by
given by
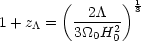
|
At a time before the discovery of the cosmic expansion by Hubble,
Einstein proposed that the Universe could be static if there was such
a  term, and that
the value of
term, and that
the value of  would determine the cosmic
density. The later discovery of the cosmic expansion did not, however,
cause people to drop the
would determine the cosmic
density. The later discovery of the cosmic expansion did not, however,
cause people to drop the
 term from the
equations.
term from the
equations.
We can integrate (14) once. Using the conservation of matter expressed
as  =
=
 a-3 (equation 7), we get
a-3 (equation 7), we get
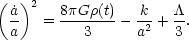
|
The  version of
equation (13) follows by evaluating the integration
constant k (the curvature constant) at the present epoch:
version of
equation (13) follows by evaluating the integration
constant k (the curvature constant) at the present epoch:
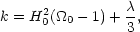
| (15) |
to give
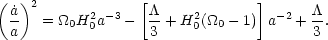
| (16) |
A universe with k = 0 is said to be "flat". If
 = 0, then the
flat universe is a
= 0, then the
flat universe is a
 = 1 universe (the
Einstein de Sitter model). There is
a considerable body of opinion in favour of k = 0, but until the idea
of an early "inflationary" phase of expansion was introduced by Guth,
the reasons for favouring such a model were largely
aesthetic. Inflation generally demands k = 0. (There was an argument
that large scale structures would have to form very early
(z >
= 1 universe (the
Einstein de Sitter model). There is
a considerable body of opinion in favour of k = 0, but until the idea
of an early "inflationary" phase of expansion was introduced by Guth,
the reasons for favouring such a model were largely
aesthetic. Inflation generally demands k = 0. (There was an argument
that large scale structures would have to form very early
(z >  0-1) if
0-1) if
 0 were
small. Since we see the quasar population growing to a
maximum more recently than a redshift of 3, this would suggest a
relatively recent formation epoch for galaxy clusters if we could
think of some argument relating QSO activity to the origin of
clusters! We have in fact no direct evidence as to when the first
large scale structures formed.)
0 were
small. Since we see the quasar population growing to a
maximum more recently than a redshift of 3, this would suggest a
relatively recent formation epoch for galaxy clusters if we could
think of some argument relating QSO activity to the origin of
clusters! We have in fact no direct evidence as to when the first
large scale structures formed.)
Note that we can introduce a dimensionless measure of
 :
:
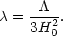
| (17) |
Then the curvature constant, k becomes
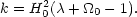
|
The k = 0 flat universe such as implied by inflationary theories therefore has
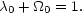
|
If we argued that the dark matter was all baryonic, contributing
 0 = 0.2,
then we would need
0 = 0.2,
then we would need
 = 0.8 for consistency
with standard inflationary scenarios.
= 0.8 for consistency
with standard inflationary scenarios.
The coasting redshift in terms of
 is
is
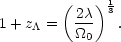
| (18) |
For values of  such as
those described above for a flat universe we
see a coasting period at relatively recent redshifts
z
such as
those described above for a flat universe we
see a coasting period at relatively recent redshifts
z
 1 - 2.
1 - 2.
Current thinking on the issue of whether
 should be there
or not varies over a short timescale of a few years. There is certainly no
observational evidence for including the
should be there
or not varies over a short timescale of a few years. There is certainly no
observational evidence for including the
 term in the
equations. From the point of view of our limited understanding of the
status of the
Einstein Field Equations in Quantum Field theory, there is every
reason to want it to be exactly zero. However, it brings an extra
parameter into the cosmological model and an extra degree of freedom
with which to fit the observations. Thus we often see it being brought
in at a time when there appear to be difficulties in explaining a set
of observations.
term in the
equations. From the point of view of our limited understanding of the
status of the
Einstein Field Equations in Quantum Field theory, there is every
reason to want it to be exactly zero. However, it brings an extra
parameter into the cosmological model and an extra degree of freedom
with which to fit the observations. Thus we often see it being brought
in at a time when there appear to be difficulties in explaining a set
of observations.
A notable example of "wheeling in the cosmological constant" was in
the case of explaining why there were so many more Quasars having a
redshift near to 2 than might have been expected. This could be
explained by putting the coasting period at a redshift of 2
(Petrosian, Salpeter and
Szekeres, 1967).
More recently, it has been
noticed that certain standard models for galaxy formation do not have
enough clustering on the largest scales. This might be explained in
part by the dynamical influence
 could have on the
formation of large scale structure
(Efstathiou, Sutherland and
Maddox, 1990;
Lahav et al. 1991).
could have on the
formation of large scale structure
(Efstathiou, Sutherland and
Maddox, 1990;
Lahav et al. 1991).