1.4. The Value of ₀

The luminous matter itself accounts for only _lum ~ 0.005h² (Faber and Gallagher, 1979). This was discovered long ago to be insufficient to account for either the flat rotation curves of disk galaxies (the dark massive halo problem, Rubin (1988)), or for the velocity dispersions of groups and clusters of galaxies (the virial mass discrepancy problem, Zwicky (1933)). It later became apparent from cosmic nucleosynthesis arguments that the baryonic density of the universe was substantially higher than the density inferred from the luminous material. There is "dark (nonluminous) baryonic material" in some form or other, perhaps warm gas, or even very low luminosity stars. The amount of baryonic dark matter inferred from nucleosynthesis appears to be just about enough to explain the cluster virial mass discrepancy problem in most clusters of galaxies. However, this would not be sufficient to make ₀ = 1. Whether we care about ₀ 1 is a central issue of cosmology, so I shall discuss briefly the various ways we get at ₀ and why we should strive to get ₀ = 1.

But first a word of caution which we will continually return to throughout these lectures. Determinations of ₀ are frustrated by the fact that ₀ describes the quantity of gravitating matter in the universe, whereas we only see the luminous material which is but a fraction of the total mass density. If the luminosity density were everywhere proportional to the mass density, this would not prove a problem since it would only be necessary to discover what the sealing factor is. However, it is evident that the mass and light are distributed differently on different scales and some other hypothesis is needed.

The simplest hypothesis of this kind is that the fluctuations in mass density about the mean are proportional to the fluctuations in light density. The constant of proportionality is referred to as the biasing parameter and it is denoted by the symbol b. We shall encounter this frequently in what follows. Note that the constancy of the biasing parameter is merely a simplifying hypothesis, the actual situation could be far more complicated.

1.4.1. The Deceleration Parameter q₀

The central task of classical cosmology was to determine the cosmic expansion rate, H₀ and the deceleration parameter q₀:

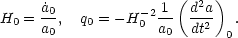
(19)

H₀ was seen as the slope of the velocity-distance relationship and q₀ as the deviation from the linear Hubble law, its curvature, due to the gravitational deceleration of the cosmic expansion.

Note that by virtue of equation (5) and the definition of ₀ (equations (11) and (12))

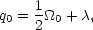
(20)

with = / 3H₀². This relationship between ₀ and q₀ holds only as long as equations (5, 6, 7) or (14) are valid; that is, provided there is no cosmic pressure. The Einstein de Sitter universe has q₀ = 1/2 (since = 0 and ₀ = 1).

We can calculate the relationships between the redshift of a galaxy and various observed properties such as brightness, look-back time and surface brightness. For example, the look-back time, measuring the time elapsed since photon was emitted at time t_E, to redshift z is

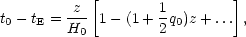
(21)

for small z.

The apparent brightness l is related to the intrinsic luminosity L by

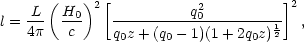
(22)

and for not too distant galaxies (z < 1), this simplifies to

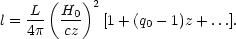
(23)

This expression is also exact in the limits q₀ = 0 and q₀ = 1. The first terms are simply the standard r^-2 inverse square law, the correction due to the q₀ term is due to the deceleration of the expansion. In astronomical units this is

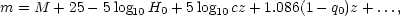
(24)

where m is the apparent magnitude of a galaxy of absolute magnitude M seen at a redshift z. (Technically, these are the luminosities or magnitudes integrated over the whole spectrum of the emitted light. If the measurements are done in a restricted spectral band, then other terms come into this relationship, these are the so-called K-correction terms). This expresses the Hubble Law directly in terms of a magnitude-redshift relationship.

Note that any intrinsic evolution of the quantity L (or the absolute magnitude M) will introduce non-geometric effects into the relationship and so confuse the determination of q₀. We can approximate this by assuming that the luminosity evolves as

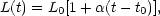
(25)

when expressed as a function of look-back time t - t₀. Relating look-back time to redshift then yields

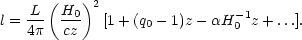
(26)

showing an extra linear dependence on z. Thus if this relationship is used to measure q₀, the (unknown) evolutionary correction biases q₀ downward by H₀^-1.

In the small z limit, we can also calculate the number of galaxies N(m) we would see in a galaxy survey down to apparent magnitude m, again under the assumption that there are no evolutionary effects. This is the classical number-magnitude relationship.

In the pre-1965 days of cosmology the central issue in cosmology was the values of H₀ and q₀. Cosmology was simply "a search for two numbers". Today, that view has changed. Cosmology is properly a branch of physics and the values of these two parameters are regarded simply as important parameters that observations will eventually determine to characterize our Universe.

Unfortunately, the program of measuring the curvature of the Hubble Law directly has not provided any strong constraints on q₀. This is largely because the curvature of the relationship is influenced by non geometric effects (galaxy luminosities evolve with time in an unknown way) and because there is considerable scatter in the magnitude-redshift diagram. Indeed, the tendency today is to use the Hubble diagram and the number-magnitude relationship together to determine the evolutionary history of galaxies! (See Guideroni and Rocca-Volmerange, 1990; Rocca-Volmerange and Guideroni, 1990). As we shall see below, there is a possibility that this will yield limits on ₀ and as a by-product since faint galaxy counts are sensitive to ₀.

1.4.2. The classical approach again

In order to discriminate cosmological models, the magnitude redshift relationship needs a large sample of redshifts out to at least z = 0.5 and preferably as far beyond z = 1 as possible. Loh and Spillar (1986) have used a galaxy survey to determine approximate redshifts for ~ 1000 galaxies out to a redshift of z ~ 1. On the basis of this survey, they look at the redshift-volume relationship and conclude that ₀ = 0.9 ± 0.3 if = 0. Caditz and Petrosian (1989) argue that the luminosity function history assumed by Loh and Spillar is not consistent with their data. Taking this into account, Caditz and Petrosian derive ₀ 0.2 with considerable uncertainty due to such things as incompleteness of the sample. Yoshii and Takahara (1989) make a detailed model for the luminosity evolution based on merger driven evolution and discuss the problems associated with such methods of getting at ₀.

The number magnitude relationship provides an alternative probe of cosmological models and galaxy evolution and has generated a great deal of interest since we can now survey galaxies down to extremely faint magnitudes in many wavebands. In recent years we have seen faint galaxy counts by Tyson (1988) and by Jones et al. (1991) and Metcalf et al. (1991). The latter surveys penetrate to B-magnitudes B < 25. The interpretation of such counts and the galaxy evolution models that are used have been discussed by Koo (1990) and by Guideroni and Rocca-Volmerange (1990). It seems that the present data in the R and B bands can be largely understood in terms of current models of galactic evolution. However, Cowie (1991) has recently presented some infrared counts of galaxies which confuse the situation somewhat by appearing to demand a non-zero cosmological constant! This is also the conclusion of the analysis of counts by Fugikita et al. (1990).

1.4.3. Cosmic Nucleosynthesis

Cosmic nucleosynthesis sets strong bounds on the amount of baryonic material in the Universe (Boesgard and Steigman, 1985; Pagel 1991a, b). Standard Big Bang nucleosynthesis implies that

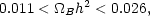
(27)

where _B is the contribution of baryons to the total mass density. (See chapter 4 of the Kolb and Turner (1990) book for an excellent discussion of this). There is a need already here to have ten times as much mass in the baryonic dark matter as is accounted by the luminous mass in galaxies.

The nucleosynthesis question is fully discussed elsewhere in this volume. There is a couple point that should be emphasised here. The low baryonic density implied by nucleosynthesis causes a problem in the hydrogen-helium cooling of the pregalactic gas: the density may simply be too low. This is a point about star formation, but it does have a bearing on what we observe on the largest scales since we can only observe what is luminous.

1.4.4. ₀ from Hubble flow deviations

The large scale peculiar motions of galaxies are clearly related to the density inhomogeneities, since it is those inhomogeneities that give rise to the peculiar motions. is involved in that relationship and so in principle it could be estimated by comparing density excursions with peculiar velocities. The problem arises because we cannot directly observe the fluctuations in mass density, but only the fluctuations in luminosity density. Another parameter relating mass density fluctuations to luminosity density fluctuations comes into the game. This parameter, b, is called the bias parameter and it might depend on the location, the morphological type of the galaxies involved, or any number of other things. In this spirit of ignorance the simplest assumption we can make is that b is a universal constant. Then we can in principle determine the combination ₀ b^-5/3. We shall have more to say about this below (see sections 2.1.3 and 4.2.1).

On the assumption that light traces mass (b = 1), most dynamical determinations of ₀ converge on 0.1 < ₀ < 0.3 (Peebles, 1987; Shanks et al., 1989). Stavely-Smith and Davies (1989) report ₀ = 0.08 ± 0.05. (The latter authors remark that some `biasing' is demanded by their data, bringing ₀ up to at least 0.25.)

More recently, deep redshift surveys of galaxy samples drawn from the IRAS catalog have provided another route to ₀. The limits from these surveys involve another parameter, b, the biasing parameter, whose value is largely unknown (and may not even be a constant):

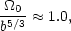
with large error bars. More will be said about this approach later on (section 2.3.2).