1.5. = 1, Dark Matter and Inflation

There is no compelling direct observational evidence for ₀ = 1. The driving force behind the notion that ₀ = 1 is undoubtedly the inflationary picture for the early universe (see the review of Brandenburger, 1990). Not only does this picture have appeal in providing answers to some fundamental questions (like the horizon problem), but it seems almost inevitable from the point of view of our present knowledge of high energy physics. That weighs more strongly in favour of adopting ₀ = 1 than the lack of any obvious candidate particle weighs against the notion.

1.5.1. Flatness and Inflation

It is interesting to write down and solve the equation for the evolution of the density parameter (t) with time (Ducloux, 1989). Suppose the matter in the universe has density and pressure p such that

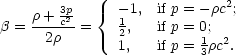
The case p = 0, = 1/2 is relevant to the current epoch, while the radiation gas case p = 1/3c², = 1 is relevant to the early universe. The interesting very early universe case p = - c² corresponds to = - 1.

A not inconsiderable amount of work gives the evolution of as

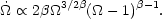
The simplest case = 1 is relevant to the current era and the solution is then trivial:

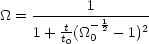
Thus in order to get ₀ = 0.1 today, we need _P = 1 - 10^-60 at the Planck time t_P ~ 10^-60t₀. It is the fact that should have been so incredibly close to 1.0 initially that is referred to as the "fine tuning" problem. The argument goes then that it was so close it must (sic) have been exactly 1.000 ... . The alternative is to seek a mechanism whereby such a value might be generated. The mechanism is "inflation".

In its simplest form the idea of inflation is as follows. If at an early stage the universe had equation of state

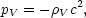
the cosmic expansion would be exponential:

The fact that the pressure p_V is negative is a consequence of the physics of the vacuum at the high temperatures prevailing in the early universe.

The exponential expansion phase is referred to as the "de Sitter phase" and would continue for as long as the material had this peculiar equation of state. The universe then makes a transition to an expansion for a "normal" equation of state. It turns out that during this "de Sitter" expansion phase, very distant parts of the universe are causally connected. This is presumed to be an "explanation" for the flatness problem, the idea being that all anisotropies and inhomogeneities disappear during this phase of phenomenal expansion.

The other side of the coin is that it is necessary to generate some primordial inhomogeneities that will eventually give rise to the formation of galaxies and large scale structure. These must be generated during or after the inflationary era and are generally thought to arise out of quantum fluctuations in the vacuum state. In the simplest models the spectrum of fluctuations is the Harrison-Zel'dovich spectrum with Gaussian distributed fluctuations (Guth and Pi, 1985). We now appear to have evidence that this spectrum does not have enough large scale power to explain the observations of large scale structure. (See Kashlinsky and Jones (1991) for arguments that the spectrum is not Harrison-Zel'dovich).

There is however no lack of alternate (albeit somewhat ad hoc) model which allow us to get around the problem of the lack of large scale power in the Harrison-Zel'dovich spectrum. One of the most plausible ways around this is by generating non-Gaussian fluctuations. Chaotic inflation (Linde, 1984, Linde and Mukhanov, 1987) can generate non-Gaussian fluctuation (Matarrese, Ortolan and Lucchin, 1989; Yi, Vishniac and Mineshige, 1991). Strong claims have been made for models involving "global texture" as these also generate non-Gaussian initial fluctuations (Spergel et al., 1991).