


2.5. Clusters and Voids
Rich galaxy clusters are prominent features on sky survey plates, but objects like the Coma cluster of galaxies are rather rare. According to Bahcall and Soneira (1983) the density of richness R > 0 clusters is nR > 0 = 7.5 × 10-7 Mpc-3. Abell (1958) catalogued these, and that catalogue has since been extended to the southern sky by Abell, Corwin and Olowin (1989). These clusters are selected in projection and it is rather difficult to assess the selection effects that go into making up such catalogues. Redshifts are now available for large numbers of Abell clusters (see, for example, Huchra et al., 1990).
Searching for clusters in three dimensional redshift surveys of galaxies was initiated by Geller and Huchra (1983) and then refined by using N-body simulations by Nolthenius and White (1987) and by Moore (1991). Such objective catalogues are very useful in a number of respects, especially when looking at the group/cluster multiplicity or luminosity function, or when calculating a cluster-cluster correlation function.
Moore (1991) calculates the distribution of cluster luminosities rather than the multiplicity function. The cluster luminosities can be related to their masses through an assumed Mass to Light ratio, and thence directly to theories for the origin of large scale structure. Moore's main result is that the distribution of cluster luminosities derived from the CfA catalogue is best fit by
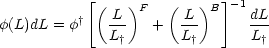
|
where F = 1.16 ± 0.07 is the faint end slope,
B = 1.7 ± 0.12 is the
bright end slope, and L† is a characteristic
luminosity corresponding to absolute magnitude
M† = - 22.2 ± 0.2. The normalization is
given by
 † = 3.0
± 0.5 × 10-4 Mpc-3. At the end, a
standard Schechter-Type luminosity function would be far too steep.
† = 3.0
± 0.5 × 10-4 Mpc-3. At the end, a
standard Schechter-Type luminosity function would be far too steep.
Another interesting aspect of galaxy clusters is the distribution of
velocity dispersions. The Abell clusters show a rather flat
distribution: n  exp(-3V1000), where V1000 is the
cluster velocity
dispersion on units of 1000 km s-1, showing the existence of a
substantial number of clusters with velocity dispersion in excess of
1000 km s-1
(Frenk et al, 1990).
These authors suggested that the high
velocity dispersions could be due to contamination by nonmember
galaxies or superposed clusters. This is a claim that will only be
resolved when we have a ROSAT generated galaxy cluster catalogue. The
groups identified by
Moore (1991)
in the CfA catalogue have a much
steeper distribution of velocity dispersions
n
exp(-3V1000), where V1000 is the
cluster velocity
dispersion on units of 1000 km s-1, showing the existence of a
substantial number of clusters with velocity dispersion in excess of
1000 km s-1
(Frenk et al, 1990).
These authors suggested that the high
velocity dispersions could be due to contamination by nonmember
galaxies or superposed clusters. This is a claim that will only be
resolved when we have a ROSAT generated galaxy cluster catalogue. The
groups identified by
Moore (1991)
in the CfA catalogue have a much
steeper distribution of velocity dispersions
n  exp(-15V1000). The
two distributions are equal around
V1000 = 600 km s-1. Most of the
groups found in the CfA catalogue would not qualify as Abell clusters,
they are not dense enough. What is interesting is that the CDM
predictions for a bias parameter b = 2 - 2.5 produce reasonable
agreement with the CfA group data.
exp(-15V1000). The
two distributions are equal around
V1000 = 600 km s-1. Most of the
groups found in the CfA catalogue would not qualify as Abell clusters,
they are not dense enough. What is interesting is that the CDM
predictions for a bias parameter b = 2 - 2.5 produce reasonable
agreement with the CfA group data.
As a final comment on clusters of galaxies, it should be remarked that the original de Lapparent slice contained an unusually large number of Abell clusters (A2162, A1267, A1185, A1213 and A617 besides A1656, the Coma cluster). Thus the CfA slice is rather special in this respect, especially in comparison with equivalent southern hemisphere slices (da Costa, 1991).
2.5.2. The Cluster-Cluster Correlation Function
The cluster-cluster correlation function
(Klypin and Kopylov, 1983;
Bahcall and Soneira, 1983;
Bahcall, 1988a,
b)
is a power law falling to unity on scales
r0  25h-1 Mpc. and remaining positive
beyond 50h-1
Mpc. Taken at face value, this provides a strong argument against CDM
models. Not only does CDM fail to predict such a large correlation
length, r0, the correlation length in CDM is depends
only on the shape of the power spectrum and not its amplitude and hence the
cluster-cluster correlation length is independent of the value of the
bias parameter. This last point makes it difficult to fix CDM without
saying the data has been wrongly interpreted.
25h-1 Mpc. and remaining positive
beyond 50h-1
Mpc. Taken at face value, this provides a strong argument against CDM
models. Not only does CDM fail to predict such a large correlation
length, r0, the correlation length in CDM is depends
only on the shape of the power spectrum and not its amplitude and hence the
cluster-cluster correlation length is independent of the value of the
bias parameter. This last point makes it difficult to fix CDM without
saying the data has been wrongly interpreted.
Both Soltan (1988)
and Sutherland (1988)
have found evidence for
strong anisotropies in the correlation function of clusters looked at
in redshift space. They argued that projection effects enhance the
apparent richness of galaxy clusters and so conspire to boost
 cc. The
real lengthscale according to these critics is
r0
cc. The
real lengthscale according to these critics is
r0  14h-1 Mpc. A simple model for this was presented by
Dekel et al. (1989a,
b),
though the later study of the phenomenon by
Sutherland and Efstathiou
(1991)
shows that the reasons are not so simple.
14h-1 Mpc. A simple model for this was presented by
Dekel et al. (1989a,
b),
though the later study of the phenomenon by
Sutherland and Efstathiou
(1991)
shows that the reasons are not so simple.
The anisotropies reported by Soltan and by Sutherland amount to peculiar velocities ~ 2000 km s-1. It is difficult to see how they could be accounted for entirely by the relative motions of galaxies clusters as supposed by Bahcall (1988) and her collaborators since Hubble flow deviations as large as ~ 600 km s-1 are rare (Lucey and Carter, 1988).
There appears to be a trend in the amplitude of the cluster-cluster correlation function with cluster richness in the sense that the richest clusters have the greatest correlation lengths (see for example Bahcall and Soneira, 1983 and Bahcall, 1988). However, groups of galaxies selected from the CfA catalogue (Nolthenius and White, 1987; Moore, 1991) have a correlation function that agrees in amplitude and slope with the predictions of CDM. Given that the prediction of CDM is independent of bias parameter, and that the group selection algorithm seems to be quite effective (and objective), this must be regarded as a plus point for CDM. The disease could well be in the Abell cluster catalogue and we must await surveys based on the ROSAT satellite to give an alternative rich galaxy cluster catalogue.
The Bootes void (Kirshner et al., 1981) with diameter ~ 60h-1 Mpc was the first void to attract attention.e of the universe is bubble-like and entirely dominated by the voids and their walls. The bubble-like appearance may be an artifact of peculiar velocities distorting the real map of galaxy distribution (Kaiser, 1988). However, the velocities are unlikely to significantly reduce the (large) size of typical voids which should be explained by any successful theory for formation of the large-scale structure in the Universe. Nor are the voids a consequence of extreme luminosity segregation (Dekel and Silk, 1986): the distribution of low surface brightness galaxies (Thuan et al., 1987, 1991) and of IRAS galaxies (Babul and Postman, 1990) follows that of bright ones.
Einasto, Einasto and Gramman (1989) have studied a compilation of voids, and found that their mean radius is ~ 50h-1 Mpc. However, more recently, Kauffmann and Fairall (1991) applied a void finding algorithm to various redshift catalogues and found that the distribution of void diameters for their void catalogue peaked in the range 8-11 h-1 Mpc., with a long tail in the distribution extending to voids the size of the Bootes void or larger. It is not known whether these voids are truly empty of material. Einasto et al. conclude, on the basis of their numerical simulations (which included a cosmological constant), that one third of the material in the universe could reside in the voids. The void radii are sensitive to the bias level applied to the simulation, so this may be a good way to fix the bias parameter b.
As a final comment, it should be noted that the distribution of rich Abell clusters also reveals large voids. There are two unusually large voids in the northern sky Abell catalogue (Bahcall and Soneira, 1983; Huchra et al., 1990). This is interesting in relation to the Voronoi clustering model for Abell clusters (van de Weygaert, 1991) which purports to provide an explanation for the regularity in the redshift distribution of galaxies in pencil beam surveys (Broadhurst et al., 1990) since that model is normalized relative to the rich cluster distribution. The voids in the Voronoi model are on average 125h-1 Mpc. across and these presumably correspond to the voids seen in the Abell catalogue.