


2.4. Surveys with Independent Distance Estimates
Having samples of galaxies for which there are distance estimates that are independent of the Hubble law is of crucial importance. It is true that such samples are necessarily considerably smaller than the redshift survey samples, numbering at most in the thousands of galaxies. There are of course strong selection effects in creating such samples. These arise out of the fact that properties of particular types of object are exploited to give the distance estimator. Thus there are different distance indicators for elliptical galaxies, for spiral galaxies in general, and for particular classes of spiral galaxy. The distance errors are generally very large (at least 20-30%) unless one focusses on a special type of galaxy of known luminosity (standard candles), and then there are hidden dangers as exemplified by the original Rubin-Ford sample of ScI galaxies (see section 2.4.1).
The analysis of such data sets is also non-trivial. One is tempted to fit models of clusters with power law halos, but that specific model fitting is fraught with dangers. What, for example, is the significance of a result obtained through a model that does not in fact represent the data? Bertschinger and Dekel have, in a series of important papers, described a method for reconstructing the full three dimensional distribution of galaxies and their flow relative to the cosmic background. Their technique, "POTENT", makes a plausible assumption about the nature of the velocity field that is being probed, and is potentially capable of giving us a good smoothed picture of what is going on in the Universe.
I shall discuss some data samples that have independent distance estimators, and then go on to discuss the Bertschinger-Dekel technique.
The pioneering work of Rubin et al. (1976a, b) used a sample of ScI galaxies arguing that these were good "standard candles" whose true distances could be estimated from their apparent brightness alone. Their catalogue of 18 galaxies was pruned to reduce various biases to a sample of 96 objects having radial velocities in the range 3500 km s-1 to 6500 km s-1. On analyzing the distribution of "true distance" relative to Hubble flow distance they found substantial motion of the Local Group of galaxies relative to their sample of distant ScI galaxies.
The Rubin et al. analysis yielded a Local Group mass center velocity of VRF = 454 ± 125 km s-1 towards l = 163° and b = - 11° relative to the ScI sample. The Microwave Background Radiation dipole anisotropy implies a motion of the mass center of the Local Group of VMWB = 610 ± 50 km s-1 towards l = 265° and b = 480° relative to the cosmic frame (Smoot et al., 1991). These numbers take account of the motion of the Sun relative to the mass center of the Local Group V = 295 km s-1 towards l = 97° and b = - 6°. The conclusion is thus that the ScI galaxy sample as a whole is moving with velocity V = 885 km s-1 towards l = 304° and b = 26° relative to the frame of reference in which the microwave background radiation is isotropic.
The Rubin-Ford effect has been the subject of intense discussion ever since it was reported (Fall and Jones, 1976; Hart and Davies, 1982; Collins, Joseph and Robertson, 1986; James, Joseph and Collins, 1991). I still think that this particular data set is indeed biased in the way described by Fall and Jones and the apparent large scale flow implied by that data is spurious. This particular bias arises only in samples of galaxies selected in a narrow range of absolute magnitudes, such as ScI galaxies and so one should be careful before arguing that such effects arise in other samples.
2.4.2. Samples of Elliptical Galaxies
For determining redshift independent distances to elliptical galaxies
one can use a Faber-Jackson
(Faber and Jackson, 1976)
type relation
between the isophotal diameter Dn of the galaxy where
the surface
brightness falls to some particular value and central velocity
dispersion,  0.
The relationship,
Dn
0.
The relationship,
Dn 
 4/3 which was
found by
Dressler et al. (1987)
and Lynden-Bell et
al. (1988)
has been the subject of much discussion
(Djorgovski and Davies,
1987;
Lucey and Carter, 1988;
de Carvalho and Djorgovski,
1989).
4/3 which was
found by
Dressler et al. (1987)
and Lynden-Bell et
al. (1988)
has been the subject of much discussion
(Djorgovski and Davies,
1987;
Lucey and Carter, 1988;
de Carvalho and Djorgovski,
1989).
Lynden-Bell et al. (1988) (generally referred to as "S7") have applied this distance indicator to a sample of ~ 400 elliptical galaxies with the rms depth of 6,000 km s-1 and find a large peculiar velocity of 600 ± 100 km s-1 on a scale of ~ 50h-1 Mpc. The direction of this velocity vector is towards the Hydra-Centaurus system. This direction roughly coincides with the microwave background dipole direction, the dipole determined from spiral galaxy samples and the optical light dipole direction (Lahav, 1987). It also coincides roughly with the long axis of the quadrupole component of the local velocity field (Lilje, Yahil and Jones, 1986).
The discovery of bulk motions relative to the cosmic frame provided by the microwave background radiation, and of a coherent infall towards the direction of the Hydra-Centaurus part of the sky is of considerable importance. We discuss these in later sections.
A word of caution should be in order here: the new distance
indicator was established by using only elliptical galaxies in the
Coma cluster of galaxies. One knows, and generally
expects, galaxy
properties to be influenced by their environments (tidal interactions,
mergers, gas removal etc. - see the review of
Dressler (1984)).
One cannot be sure at this stage whether the
(Dn,  relation applies
equally to elliptical galaxies in other environments. Of the ~ 400
ellipticals in the S7 sample, a third are in rich
clusters, a third in
poor ones and a third in the field. However the sample is not large
enough to estimate the contribution from these environmental effects
or other likely evolutionary effects
(Djorgovski, de Carvalho and
Han, 1988;
Silk, 1989).
Much of the future discussion will turn around the
quality of the distance indicator for elliptical galaxies.
relation applies
equally to elliptical galaxies in other environments. Of the ~ 400
ellipticals in the S7 sample, a third are in rich
clusters, a third in
poor ones and a third in the field. However the sample is not large
enough to estimate the contribution from these environmental effects
or other likely evolutionary effects
(Djorgovski, de Carvalho and
Han, 1988;
Silk, 1989).
Much of the future discussion will turn around the
quality of the distance indicator for elliptical galaxies.
2.4.3. Samples of spiral galaxies
For disk galaxies there is the Tully-Fisher relationship (Tully and Fisher, 1977) between the total luminosity and the asymptotic rotational velocity width of the 21 cm. HI line. This has been applied at a variety of wavelengths from the blue to the infrared (Aaronson et al., 1986; Stavely-Smith and Davies, 1989).
These samples of spiral galaxies have been used for a variety of purposes, though in general because of the inaccuracy of the distance estimator the data is best smoothed over relatively large volumes. (See Hesslbjerg-Christiansen (1991) for a potentially important way of improving these distance estimates). They have been used to rederive the motion of the local sample of galaxies relative to the microwave background, and to determine the quadrupole distortion of that flow (Lilje et al., 1986; Stavely-Smith and Davies, 1989). They have also been used to map out the motions of galaxy clusters relative to one another, since good estimates of distances to clusters can be obtained by averaging distance estimates for a number of cluster members.
The relative motions of clusters of galaxies was studied by
Aaronson et al. (1986,
1989)
by determining redshift independent distances to
individiual member galaxies in some 11 clusters. They recovered a
large scale flow of the Local Supercluster towards the direction that
is now identified with the Great Attractor. What seems significant
about their result is that the Hubble flow deviations are relatively
small ( 300 km
s-1) when measured from clusters of galaxies.
300 km
s-1) when measured from clusters of galaxies.
A recent detailed discussion by
Lucey et al. (1991)
using the elliptical galaxies in dusters (and the
Dn -  elliptical
galaxy distance indicator) confirms that the Hubble flow deviations for
galaxy clusters are generally small, but that there are a few
outstanding cases where there is an indication of substantial
non-Hubble motion, particularly the cluster A2634. However, the
authors comment that tidal stripping among galaxies in the central
regions of this cluster may have been responsible for the apparent
non-Hubble component of the flow.
elliptical
galaxy distance indicator) confirms that the Hubble flow deviations for
galaxy clusters are generally small, but that there are a few
outstanding cases where there is an indication of substantial
non-Hubble motion, particularly the cluster A2634. However, the
authors comment that tidal stripping among galaxies in the central
regions of this cluster may have been responsible for the apparent
non-Hubble component of the flow.
2.4.4. The "Real" 3-Dimensional Distribution
Early studies of non-Hubble motions used fitted specific models for the Great Attractor and its environment (Lynden-Bell et al. 1988). While such models give an indication of what the Great Attractor is, one is left with a very large parameter space of possible models none of which has an a priori dynamical justification.
This model-fitting situation has been dramatically improved by the recent discovery of Bertschinger and Dekel (1989) that one could, on the basis of a few reasonable assumptions, reconstruct the entire three dimensional velocity field given only the radial peculiar velocity data for a sample of galaxies. Moreover, the sample does not have to be a complete sample (though where there are most galaxies the reconstruction of the cosmic flow field is obviously most reliable). Bertschinger, Dekel, Dressler and Faber (1991) in a recent series of papers, have applied the technique to a compendium of redshift samples that allow the universe to be mapped out to a distance of 6000 km s-1.
The actual argument describing how to do this is quite complex, but it can be simplified for didactic purposes by taking a liberty with the coordinate systems being used.
Given a galaxy with radial velocity cz and velocity independent distance estimate r, the peculiar radial velocity is
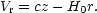
| (44) |
If we suppose that Vr is the radial component of a
vector field V that is the gradient of a potential
 , we can write
, we can write
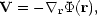
| (45) |
and this has solution
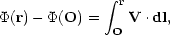
|
where O represents the observer (us). The integral can be taken over
any path from O to r, and in particular a radial path. This
particular
choice of path involves only the radial component of the velocity,
which we know. In r-space spherical polar coordinates
(r,  ,
,
 ):
):
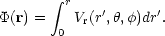
| (46) |
We have set the potential equal to zero at the origin since we don't
need its value, only its derivatives. Having got
 at all points we
can then determine the three-dimensional velocity field from it by
doing
at all points we
can then determine the three-dimensional velocity field from it by
doing
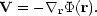
| (47) |
The projection of this velocity along the line of sight is the contribution of the peculiar velocity to the observed recession velocity. Thus we can improve our estimate of the true distance to the galaxy.
We seem to have got something for nothing! In fact it was not for free. The price we had to pay was the assumption that the velocity field was derivable from a potential. That is why the method is called "potent".