


3.4. Genus
A promising way of classifying the structure of the universe is to see
how the topology of the surfaces of constant density in the universe
varies with the value of the density
(Gott, Melott and Dickinson,
1986;
Weinberg, Gott and Melott,
1987).
The topological genus of the
set of points enclosed by surfaces of constant density is defined as
the number of holes minus the number of isolated regions (though this
is not how it is calculated). Thus a toroidal region has a genus of -1
and an isolated sphere has a genus of 0. The genus signature of the
distribution is calculated as a function of the density threshold at
which the surfaces are defined. Several authors, starting with
Doroshkevich (1970)
calculated the genus signature for a windowed
Gaussian random density field as a function of the threshold
 defining the surfaces:
defining the surfaces:
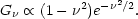
| (58) |
 is measured in terms of the
variance of the field seen through the
selected window. The constant of proportionality depends on the power
spectrum of the windowed density distribution. If the distribution is
non-Gaussian, this would show up in the genus signature.
is measured in terms of the
variance of the field seen through the
selected window. The constant of proportionality depends on the power
spectrum of the windowed density distribution. If the distribution is
non-Gaussian, this would show up in the genus signature.
This has been discussed at length in two recent papers Gott et al. (1989) and Melott et al. (1989). The main technical problem is that of relating the observed two dimensional sections of three dimensional data to the three dimensional situation. In the data paper (Gott et al, 1989), catalogues of all kinds of objects ranging from dwarf galaxies to Abell clusters are used. It is found that the universe is "sponge-like" on largest scales, with no evidence for a bubble-like structure which, it is claimed, could have been detected if present. There are voids, but they are interconnected, as opposed to being surrounded on all sides by galaxies. On smaller scales, the topology has a tendency to become "meatball-like".
Moore (1991) has looked at the QDOT redshift survey, smoothed over a variety of windows. The genus signature is clear on scales of 20h-1 Mpc. and 40h-1 Mpc. and is consistent with a Gaussian distribution of density fluctuations taken from a power law power spectrum with spectral index n = - 0.79 ± 0.35 on those scales. This appears to be a variance with the general hypothesis that the spectrum has the Harrison-Zel'dovich form on such scales, and in particular with the standard CDM models.