3.5. Multi-Fractals

The power-law nature of the two-point and higher order correlation functions on small scales is suggestive of some kind of scaling behaviour, at least in the range of scales where the power law is observed. The simplest structure that has such scaling properties is the simple fractal, first studied in this context by Efstathiou, Fall and Hogan (1979). Martínez and Jones (1990) have since shown that even in this apparent scaling regime, the distribution of galaxies is significantly more complex.

If the structure is not that of a simple fractal, what might it be? Jones et al (1988) have suggested that it may be Multifractal - that is, a distribution which over a certain range of scales can be characterized by a set of dimensions rather than just one dimension. There is scaling, albeit of a rather complex kind.

The multifractal description of the clustering process goes beyond the two-point correlation function, encapsulating all high order correlation functions in one function, D_q. The power of the technique has been demonstrated by Martínez et al. (1990) who examine the scaling structure of a number of well known clustering models and provide a variety of algorithms for calculating the dimensionality function D_q. The simplest of these is from the formulae for what is in fact the Renyi dimensions of the point set:

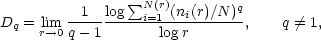
	(59)

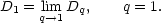
Here, n_i(r) is the count of particles in the ith cell of size r, and N is the total number of particles in all cells. There is a technical problem involved in taking the limit in a discrete sample as the cell size goes to 0.

In practise, box counting methods of determining dimensions are rather inefficient and tend to be dominated by shot noise. Van de Weygaert, Jones and Martínez (1991) have shown how to use the minimal spanning tree construct to calculate these dimensions with considerably fewer points than would be required by standard box counting methods.

The function D_q is related to the moment generating function, m_q(r) of the clustering distribution. The relationship is

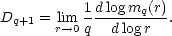
(60)

Hence each D_q encapsulates the information contained in the statistical moments of the distribution of the point set. The fact that in general one can in principle translate between the moments and the dimensions means that they contain the same information, though the information is presented in a different way. It is arguable that D - q has a more immediate physical appeal.

The simplest application of the method is to compare the Hausdorf dimension, D₀, with the Correlation Dimension, D₂. Applying this to the ZCAT redshift catalogue gives values

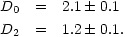
(61)

This leads to the strong conclusion that the universe is not a simple fractal characterized by one dimension. The value of D₀ indicates that the characteristic structures are sheet-like rather than filament-like. The value of D₂ is just 3 - where = 1.8 is the slope of the two-point correlation function.