This article focusses on the last two of the goals listed at the start of the previous section. The claim is that during the very early Universe, a physical process known as inflation took place, which still manifests itself in our present Universe via the perturbations it left behind which later led to the development of structure in the Universe. By studying those structures, we hope to shed light on whether inflation occurred, and by what physical mechanism.
I begin by defining inflation. The scale factor of the Universe at a given time is measured by the scale factor a(t). In general a homogeneous and isotropic Universe has two characteristic length scales, the curvature scale and the Hubble length. The Hubble length is more important, and is given by
| (1) |
Typically, the important thing is how the Hubble length is changing with time as compared to the expansion of the Universe, i.e. what is the behaviour of the comoving Hubble length H -1 / a?
During any standard evolution of the Universe, such as matter or radiation domination, the comoving Hubble length increases. It is then a good estimate of the size of the observable Universe. Inflation is defined as any epoch of the Universe's evolution during which the comoving Hubble length is decreasing
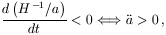
| (2) |
and so inflation corresponds to any epoch during which the Universe has accelerated expansion. During this time, the expansion of the Universe outpaces the growth of the Hubble radius, so that physical conditions can become correlated on scales much larger than the Hubble radius, as required to solve the horizon and flatness problems.
As it happens, there is very good evidence from observations of Type Ia supernovae that the Universe is presently accelerating - see the article by Schmidt in these proceedings and Ref. [2]. This is usually attributed to the presence of a cosmological constant. This is clearly at some level good news for those interested in the possibility of inflation in the early Universe, as it indicates that inflation is possible in principle, and certainly that any purely theoretical arguments which suggest inflation is not possible should be treated with some skepticism.
If the Universe contains a fluid, or combination of fluids, with energy
density 
and
pressure p, then
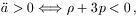
| (3) |
(where the speed of light c has been set to one). As we always
assume a
positive energy density, inflation can only take place if the Universe is
dominated by a material which can have a negative pressure. Such a
material is a
scalar field, usually denoted 
.
A homogeneous scalar field has a kinetic energy and a potential energy
V(), and has an effective
energy density and pressure given by
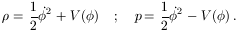
| (4) |
The condition for inflation can be satisfied if the potential dominates.
A model of inflation typically amounts to choosing a form for the
potential, perhaps supplemented with a mechanism for bringing inflation
to an end, and perhaps may involve more than one scalar field. In an
ideal world the potential would
be predicted from fundamental particle physics, but unfortunately there
are many proposals for possible forms. Instead, it has become customary
to assume that the potential can be freely chosen, and to seek to
constrain it with observations. A suitable potential needs a flat region
where the potential can
dominate the kinetic energy, and there should be a minimum with zero
potential energy in which inflation can end. Simple examples include
V = m2
2 / 2
and V = 
4,
corresponding to a massive field and to a
self-interacting field respectively. Modern model building can get quite
complicated - see Ref.
[3] for a review.