


By far the most important aspect of inflation is that it provides a possible explanation for the origin of cosmic structures. The mechanism is fundamentally quantum mechanical; although inflation is doing its best to make the Universe homogeneous, it cannot defeat the uncertainty principle which ensures that residual inhomogeneities are left over. (2) These are stretched to astrophysical scales by the inflationary expansion. Further, because these are determined by fundamental physics, their magnitude can be predicted independently of the initial state of the Universe before inflation. However, the magnitude does depend on the model of inflation; different potentials predict different cosmic structures.
One way to think of this is that the field experiences a quantum "jitter" as it rolls down the potential. The observed temperature fluctuations in the cosmic microwave background are one part in 105, which ultimately means that the quantum effects should be suppressed compared to the classical evolution by this amount.
Inflation models generically predict two independent types of perturbation:
 H2(k):
H2(k):
They are sometimes known as scalar and tensor perturbations respectively, because of the way they transform. Density perturbations are responsible for structure formation, but gravitational waves can also affect the microwave background.
We do not expect to be able to predict the precise locations of cosmic structures from first principles (any more than one can predict the precise position of a quantum mechanical particle in a box). Rather, we need to focus on statistical measures of clustering. Simple models of inflation predict that the amplitudes of waves of a given wavenumber k obey gaussian statistics, with the amplitude of each wave chosen independently and randomly from a gaussian. What it does predict is how the width of the gaussian, known as its amplitude, varies with scale; this is known as the power spectrum.
With current observations it is a good approximation to take the power spectra as being power laws with scale, so
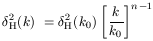
| (5) |
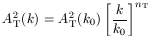
| (6) |
In principle this gives four parameters - two amplitudes and two spectral indices - but in practice the spectral index of the gravitational waves is unlikely to be measured with useful accuracy, which is rather disappointing as the simplest inflation models predict a so-called consistency relation relating nT to the amplitudes of the two spectra, which would be a distinctive test of inflation. The assumption of power-laws for the spectra requires assessment both in extreme areas of parameter space and whenever observations significantly improve.
2 For a detailed account of the inflationary model of the origin of structure, see Ref. [4]. Back.