5. PRESENT AND FUTURE

5.1. The current status of inflation

The best available constraints come from combining data from different sources; for two recent attempts see Wang et al. [1] and Efstathiou et al. [11]. Suitable data include observations of the recent dynamics of the Universe using Type Ia supernovae, cosmic microwave anisotropy data, and galaxy correlation function data such as that described by Lahav and by Frieman in these proceedings.

Currently inflation is a massive qualitative success, with striking agreement between the predictions of the simplest inflation models and observations. In particular, the locations of the microwave anisotropy power spectrum peaks are most simply interpretted as being due to an adiabatic initial perturbation spectrum in a spatially-flat Universe. The multiple peak structure strongly suggests that the perturbations already existed at a time when their corresponding scale was well outside the Hubble radius. No unambiguous evidence of nongaussianity has been seen.

Quantitatively, however, things have some way to go. At present the best that has been done is to try and constrain the parameters of the power-law approximation to the inflationary spectra. The gravitational waves have not been detected and so their amplitude has only an upper limit and their spectral index is not constrained at all. The current situation can be summarized as follows.

Amplitude _H

COBE determines this (assuming no gravitational waves) to about ten percent accuracy (at one-sigma) as approximately _H = 1.9 × 10^-5 ₀^-0.8 on a scale close to the present Hubble radius (see Refs. [12, 4] for accurate formulae).

Spectral index n:

This is thought to lie in the range 0.8 < n < 1.05 (at 95% confidence). It would be extremely interesting were the scale-invariant case, n = 1, to be convincingly excluded, as that would be clear evidence of dynamical processes at work, rather than symmetries, in creating the perturbations.

Gravitational waves r:

Measured in terms of the relative contribution to large-angle microwave anisotropies, the tensors are currently constrained to be no more than about 30%.

5.2. Prospects for the future

It remains possible that future observations will slap us in the face and lead to inflation being thrown out. But if not, we can expect an incremental succession of better and better observations, culminating (in terms of currently-funded projects) with the Planck satellite [13]. Faced with observational data of exquisite quality, an initial goal will be to test whether the simplest models of inflation continue to fit the data, meaning models with a single scalar field rolling slowly in a potential V() which is then to be constrained by observations. If this class of models does remain viable, we can move on to reconstruction of the inflaton potential from the data.

Planck, currently scheduled for launch in February 2007, should be highly accurate. In particular, it should be able to measure the spectral index to an accuracy better than ±0.01, and detect gravitational waves even if they are as little as 10% of the anisotropy signal. In combination with other observations, these limits could be expected to tighten significantly further, especially the tensor amplitude. Such observations would rule out almost all currently known inflationary models. Even so, there will be considerable uncertainties, so it is important not to overstate what can be achieved.

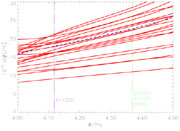
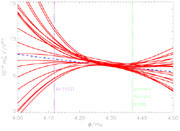
Figure 3. Sample reconstruction of a potential, where the dashed line shows the true potential and the solid lines are thirty Monte Carlo reconstructions (real life can only provide one). The upper panel shows the potential itself which is poorly determined. However some combinations, such as (dV / d) / V3/2 shown in the lower panel, can be determined at an accuracy of a few percent. See Ref. [14] for details.

Reconstruction can only probe the small part of the potential where the field rolled while generating perturbations on observable scales. We know enough about the configuration of the Planck satellite to be able to estimate how well it should perform. Ian Grivell and I recently described a numerical technique which gives an optimal construction [14]. Results of an example reconstruction are shown in Figure 3, where it was assumed that the true potential was ⁴. The potential itself is not well determined here (the tensors are only marginally detectable), but certain combinations, such as (dV / d) / V^3/2, are accurately constrained and would lead to high-precision constraints on inflation model parameters.