4. TESTING INFLATION

4.1. Quantifying microwave background anisotropies

Although the strongest tests of cosmological models will always come from the combination of all available data, for the particular purpose of constraining inflation it is likely that the cosmic microwave background anisotropies will be the single most useful type of observation, and so it is worth spending some time defining the relevant terminology.

We observe the temperature T(, ) coming from different directions. We write this as a dimensionless perturbation and expand in spherical harmonics

(7)

Again there is no unique prediction for the coefficients a_m, but they are drawn from a gaussian distribution whose mean square is independent of m and given by the radiation angular power spectrum

(8)

The ensemble average represents the theorist's ability to average over all possible observers in the Universe (or indeed over different quantum mechanical realizations), whereas an observer's highest ambition is to estimate it by averaging over the multipoles of different m as seen at our own location. The radiation angular power spectrum depends on all the cosmological parameters, and so it can be used to constrain them. To extract the full information, polarization also has to be measured.

Computation of the power spectrum requires a lot of physics: gravitational collapse, photon-electron interactions (and their polarization dependence), neutrino free-streaming etc. But as long as the perturbations are small, linear perturbation theory can be used which makes the calculations possible. A major step forward for the field was the public release of Seljak & Zaldarriaga's code CMBFAST [5] which can compute the spectrum for a given cosmological model in around one minute. An example spectrum is shown in Figure 1.

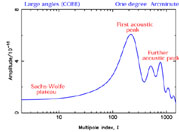
Figure 1. The radiation angular power spectrum for a particular cosmological model. The annotations name the different features, as discussed later in this article.

4.2. The key tests of inflation

In the remainder of this article, I will be interested solely in inflation as a model for the origin of structure; while it serves a useful purpose in solving the horizon and flatness problems these are no longer likely to provide further tests of the model. Indeed, the aim is to consider inflation as the sole origin of structure, since it is impossible to exclude an admixture of inflationary perturbations at some level even if another mechanism becomes favoured.

The key tests of inflation can be summarized in one very useful sentence, which lists in bold-face six key predictions that we would like to test.

The simplest models of inflation predict nearly power-law spectra of adiabatic, gaussian scalar and tensor perturbations in their growing mode in a spatially-flat Universe.

However some tests are more powerful than others, because some are predictions only of the simplest inflationary models. In what follows, it will be important to distinguish between tests of the inflationary idea itself, versus tests of different inflationary models or classes of models.

Before progressing to a discussion of the status of these tests, it is useful to define some terminology fairly precisely. In this article, a useful test of a model is one which, if failed, leads to rejection of that model. The concept of a test is to be contrasted with supporting evidence, which is verification of a prediction which, while not generic, is seen as indicative that the model is correct. A model can also accrue supporting evidence via its rivals failing to survive tests that they are put to.

4.2.1. Spatial flatness   All the standard models of inflation give a flat Universe, and this used to be advertised as a robust prediction. Unfortunately we now realise that it is possible to make more complicated models which can give an open Universe [6]. Spatial geometry therefore does not constitute a test of the inflationary paradigm, as if the Universe were not flat there would remain viable inflationary models. However the recent microwave anisotropy experiments showing good consistency with spatial flatness (see the article by Lasenby in these proceedings) provide good supporting evidence for the simplest inflation models.

4.2.2. Gaussianity and adiabaticity   If inflation is driven by more than one scalar field, there is a possibility of having isocurvature perturbations as well as adiabatic ones. The mechanism is that during inflation the other fields also receive perturbations. If they survive to the present (in particular, if they become the dark matter), this will give an isocurvature perturbation. As far as model building is concerned, such isocurvature perturbations could dominate, though this is now excluded by observations. More pertinently, the observed structures could be due to an admixture of adiabatic and isocurvature perturbations, and indeed those modes could be correlated.

Such models would also give either gaussian or nongaussian perturbations, and nongaussian adiabatic models are also possible. Whether observed nongaussianity rules out inflation depends very much on the type of nongaussianity observed; for instance chi-squared distributed fluctuations could easily be produced if the leading contribution to the perturbations is quadratic in the scalar field perturbation, while if any coherent spatial structures were seen, such as line discontinuities in the microwave background, it would be futile to try and produce them using inflation.

4.2.3. Vector and tensor perturbations   All inflation models produce gravitational waves at some level, and if seen they can provide extremely strong supporting evidence for inflation. They are not however a test, as their absence could mean an inflation model where their amplitude is undetectably small. The best way to detect them is by their contribution to large-angle anisotropies, as shown in Figure 2.

Figure 2. Scalars and tensors give different contributions to the anisotropies. While only the total spectrum is observable, provided the spectra have sufficiently simple forms this can be decomposed into the two parts, the tensors giving excess perturbations at small .

4.2.4. Growing mode perturbations   A key property of inflationary perturbations is that they were created in the early Universe and evolved freely from then. Although a general solution to the perturbation equations has two modes, growing and decaying, only the growing mode will remain by the time the perturbation enters the horizon. This leads directly to the prediction of an oscillatory structure in the microwave anisotropy power spectrum, as seen in Figure 1 [7]. The existence of such a structure is a robust prediction of inflation; if it is not seen then inflation cannot be the sole origin of structure.

The most significant recent development in observations pertaining to inflation is the first clear evidence for multiple peaks in the spectrum, seen by the DASI [8] and Boomerang [9] experiments. This is a crucial qualitative test which inflation appears to have passed, and which could have instead provided evidence against the entire inflationary paradigm. These observations lend great support to inflation, though it must be stressed that they are not able to "prove" inflation, as it may be that there are other ways to produce such an oscillatory structure [10].