4. MOND AS AN EFFECTIVE THEORY

But, on the more fundamental side, the above proximity may hint at a deep connection between cosmology and local dynamics in systems that are very small on cosmological scales. Either cosmology somehow enters and affects local laws of physics, such as the law of inertia or the law of gravity, or a common agent affects both cosmology and local physics so as to leave on them the same imprint. This would mean that MOND-and perhaps more cherished notions, such as inertia-is a derived concept, or an effective theory as we would say nowadays. An observed relation between seemingly unrelated constants appearing in a theory (in our case, a₀, the speed of light, and the radius of the horizon) may indicate that it is only an approximation of a theory at a deeper stratum, in which some of the constants do not really have any special role. A parable will help clarify the point: In experiments and observations confined to the vicinity of the earth surface, there appears a constant: the free-fall acceleration, g. If, for some reason, we were restricted to such an ant world (for example because the earth is ever clothed in a thick layer of clouds) unaware of planetary motions, universal gravity, etc., we would have looked on g as a true constant of nature. We would also notice a mysterious relation between this acceleration and two other important constants: the escape speed c_e (objects thrown with a higher velocity never return) and the radius of the earth R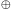. 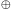This relation: g = c_e² / 2R, is practically the same as that between a₀, the speed of light, and the Hubble radius, in MOND. But, we do see beyond the earth's surface, and we do know about universal gravity, which tells us that the "constants" g and c_e actually derive from the mass and radius of the earth (hence the relation between the three). They are useful parameters when describing near-earth-surface phenomena, but quite useless in most other circumstances. In a similar vein, a₀ might turn out to be a derived constant, perhaps variable on cosmic time scales, perhaps even of no significance beyond the non-relativistic regime, where MOND has been applied so far. Its connection with the speed of light and the radius of the universe will, hopefully, follow naturally in the underlying theory that still eludes us.

Many instances of such effective theories are known. Even General Relativity is now thought to be an effective, low-energy approximation of a "higher" theory (e.g. a string-inspired theory); an idea that has been anticipated by Sakharov's "induced gravity" idea.