


Equations (1)(2) have the form of a modification of the law of inertia, but since they are algebraic relations between the MOND and Newtonian accelerations they can simply be inverted to read a = F/m = aNf (aN / a0), which seems to leave the second law intact, while modifying the Newtonian gravitational force maN to the MOND value ma. Because gravitation is the sole force that governs galactic dynamics-the only corner where the mass discrepancy has been clearly observed-existing phenomenology does not distinguish well between the interpretations of MOND as modified gravity, and modified inertia. Although there are matter of principle differences between the two interpretations (see below) they pertain to observations that are not yet available. For now we must then investigate both options.
But what exactly is meant by modifying gravity, or modifying inertia? When dealing with pure gravity the distinction is not always clear. For example, the Brans-Dicke theory may be viewed as either. But when other interactions are involved, the distinction is clear. Obviously, modified inertia will enter the dynamics of systems even when gravity is negligible, unlike the case for modified gravity. Formally, the distinction might be made as follows. In a theory governed by an action principle we distinguish three part in the action: The pure gravitational part (for example, the Einstein-Hilbert action in GR), the free action of the matter degrees of freedom (in GR it also encapsules their interaction with gravity), and the action of interactions between matter degrees of freedom. By "modifying gravity" I mean modifying the pure-gravity action; by "modifying inertia" I mean modifying the kinetic ("free") matter actions.
To understand this definition consider that inertia is what endows the motion of physical objects (particles, fields, large bodies, etc.) with energy and momentum-a currency in the physical world. Motion itself is only of a descriptive value; inertia puts a cost on it. For each kind of object it tells us how much energy and momentum we have to invest, or take away, to change its state of motion by so much. This information is encapsuled in the kinetic action.
For example, take the non-relativistic action for a system of particles interacting through gravity.
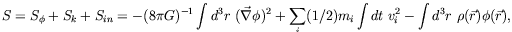
| (3) |
where
 (
(![]() ) =
) =
 i
mi
i
mi
 (
(![]() -
- ![]() ). (In GR, Sk and
Sin are lumped
together into the particle kinetic action.)
). (In GR, Sk and
Sin are lumped
together into the particle kinetic action.)
Here, modifying gravity would mean modifying
S ,
while modifying inertia would entail changing Sk.
,
while modifying inertia would entail changing Sk.