Books have been written on the "definition" of probability. We shall merely note two properties: (a) statistical independence (events must be completely unrelated), and (b) the law of large numbers. This says that if p1 is the probability of getting an event in Class 1 and we observe that N1 out of N events are in Class 1, then we have
|
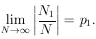
A common example of direct probability in physics is that in
which one has exact knowledge of a final-state wave function
(or probability density). One such case is that in which we
know in advance the angular distribution f (x), where
x = cos
of a certain scattering experiment, In this example one can
predict with certainty that the number of particles that
leave at an angle x1 in an interval
x1 is
Nf
(x1)x1,
where N, the total number of scattered particles, is a very large
number. Note that the function f(x) is normalized to unity:
|
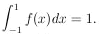
As physicists, we call such a function a distribution function. Mathematicians call it a probability density function. Note that an element of probability, dp, is
|
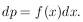