The more common problem facing a physicist is that he wishes to determine the final-state wave function from experimental measurements. For example, consider the decay of a spin-½ particle, the muon, which does not conserve parity. Because of angular-momentum conservation, we have the a priori knowledge that
|
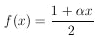
However, the numerical value of
is some universal physical
constant yet to be determined. We shall always use the
subscript zero to denote the true physical value of the parameter
under question. It is the job of the physicist to determine
0. Usually the
physicist does an experiment and
quotes a result =
* ±
. The major
portion of this report is devoted to the questions, What do we mean by
* and
? and What is the "best" way to
calculate * and
? These
are questions of extreme importance to all physicists.
Crudely speaking,
is the standard deviation,
[2] and what
the physicist usually means is that the "probability" of finding
|
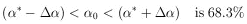
(the area under a Gaussian curve out to one standard deviation). The use of the word "probability" in the previous sentence would shock a mathematician. He would say the probability of having
|
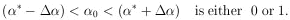
The kind of probability the physicist is talking about here we shall call inverse probability, in contrast to the direct probability used by the mathematician. Most physicists use the same word, probability, for the two completely different concepts: direct probability and inverse probability. In the remainder of this report we will conform to this sloppy physicist-usage of the word "probability."