As a first application of the maximum-likelihood method,
we consider the example of the measurement of a physical
parameter 
0,
where x is the result of a particular type of
measurement that is known to have a measuring error
. Then
if x is Gaussian-distributed, the distribution function is
|
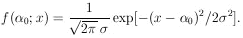
For a set of N measurements xi, each with its
own measurement
error i the
likelihood function is
|
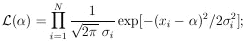
then
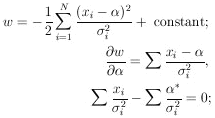
| (5) |
The maximum-likelihood solution is
| (6) |
Note that the measurements must be weighted according to the inverse squares of their errors. When all the measuring errors are the same we have
|
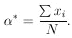
Next we consider the accuracy of this determination.