1. INTRODUCTION

1.1. The hot Big Bang

Observations of the Hubble expansion and the very isotropic microwave background suggest that the universe has evolved from an earlier state of high temperature and density (hot Big Bang) that can be reasonably well described by Friedman-Lemaitre-Robertson-Walker cosmological models. Further support for this view comes from observations of the light elements D, ³He, ⁴He and ⁷Li, which are expected to have been synthesised in significant quantities in nuclear reactions that set in about 100 seconds after the Big Bang, an effect that was first suggested by Gamow and his collaborators in the late 1940's although their aim of explaining all elements in this way could not be realised. The modern theory has been developed by Peebles (1966), Wagoner, Fowler & Hoyle (1967) and Yang et al. (1984), among others, and is described by Schramm & Wagoner (1979), Tayler (1982), Boesgaard & Steigman (1985) and Kolb & Turner (1990).

Since the mass density of radiation and relativistic particles varies with scale factor R or red-shift z as (1 + z)⁴ and that of non-relativistic matter only as (1 + z)³, the gravitating matter of the universe was dominated by the former during the first 10⁵ years or so and the universe was then in a phase with significant pressure but negligible effects from curvature or the cosmological constant (if any), and the total mass density at any one time (essentially all radiation and relativistic particles) is then fixed:

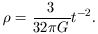
(1)

The density, in turn, fixes the radiation temperature T through the equation of state which depends on the number of relativistic degrees of freedom thermal equilibrium with photons. About ls ABB, with a temperature of th. order of 1 Mev, we have, in comparable numbers, photons, electrons, positron and N kinds of pairs of neutrinos and antineutrinos, all of which are relativistic, and a small sprinkling of non-relativistic protons and neutrons, leading t the equation of state

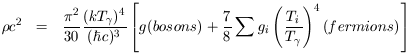
	(2)
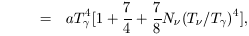
	(3)

where g, g_i represent statistical weight factors and a is the usual Stefan Boltzmann radiation density constant. The one in equation (3) comes from photons, the 7/4 from electrons and positrons and the third term from th neutrinos (and any other, hypothetical particles that might be relativistic at temperature of a few Mev and would then act like an additional contribution to N). With N = 3 and T = T, (1) and (3) lead to the temperature law (with t in seconds)

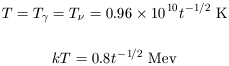
(4)

After several seconds, neutrinos have decoupled and electrons and positrons annihilate, adding entropy to the photon gas, whereafter T³ is a factor 11/4 greater than T³. After annihilation, nucleons and photons are both conserved in a co-moving volume so that their ratio = n_b / n has remained constant (a few times 10^-10) through the epoch of nucleosynthesis and to this day. Since the radiation temperature and total density are fixed functions of time, the outcome of primordial nuclear reactions (depending on particle densities and velocities as functions of time) can be expressed as a function of the one cosmic parameter , apart from physical constants which (in principle at least) can be directly measured in the laboratory.