1.2. Primordial Nucleosynthesis

Nuclear reactions set in when the temperature is down to about 0.1 Mev, since before that deuterium is prevented by photo-disintegration from building up to a sufficient abundance to allow further reactions to occur (the deuterium bottleneck). Physical constants affecting the outcome are, naturally, the relevant nuclear reaction cross-sections and two factors affecting the neutron-proton ratio at the onset of synthesis, namely N and the weak interaction constant G_F; G_F² is inversely proportional to the half-life of the neutron, _1/2, which has to be found from experiment.

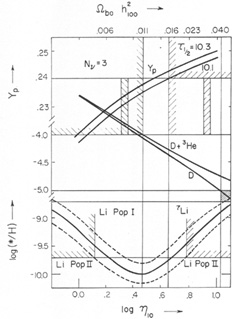
Fig. 1 shows the predicted abundances from primordial nucleosynthesis according to Standard (i.e. homogeneous) Big Bang Nucleosynthesis (SBBN) theory as a function of , or, equivalently, of _b0 h₀² where _b0 is the fraction of the cosmological closure density 3H₀² / (8G) = 1.96 × 10^-29h₀² gm cm^-3 supplied by baryons, H₀ is the Hubble constant and h₀ or h₁₀₀ the same in units of 100 km s^-1 Mpc^-1 which lies somewhere between 0.5 and 1. is related to _b0 through the known temperature of the microwave background

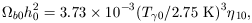
(5)

where the suffix zero refers to the present epoch and ₁₀ is in units of 10^-10. The trends in fig. 1 arise from the series of nuclear reactions starting with

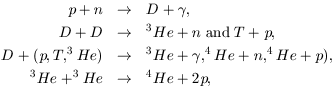
where the nuclear chain is temporarily halted because there are no stable nuclei with mass numbers 5 and 8. The main effect is to build up ⁴He with a mass fraction

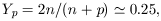
(6)

where n / p is the neutron-proton ratio at the onset of synthesis, but traces of D and ³He survive because expansion and cooling slow down nuclear reactions before their destruction is complete. The two-body character of the reactions that destroy deuterium leads to the steep decrease in its abundance with . Later traces of ⁷Li and ⁷Be are also built up, the latter eventually decaying to ⁷Li by K-capture:

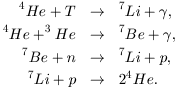
Figure 1. Primordial abundances predicted from SBBN theory after Yang et al. (1984). Olive et al. (1990) and Deliyannis et al. (1990), 7Li from the latter reference being shown with ±2 error limits, as functions of and b0 h1002. Helium abundances are given for two possible values of the neutron half-life assuming N = 3. Horizontal lines show upper limits (and a lower limit for D) based on observation and on reasonable galactic chemical evolution considerations. Tal vertical lines show the corresponding limits on the density parameters from SBBN while the shorter double vertical lines show approximate limits from midly inhomogeneous models adapted from Kurki-Suonio et al. (1990).

At low densities, the first of these reactions is the main contributor to ⁷Li and its abundance is a decreasing function of nucleon density because T and ⁷Li are both destroyed in two-body reactions. At higher densities the second reaction predominates; ³He and ⁷Be are more robust, so that the ⁷Li curve turns round and rises at higher densities leading to a minimum in the interesting range.

Helium itself increases only very slowly with because virtually all the neutrons initially present are soaked up in its production, as expressed by equation (6). However, its abundance is also significantly affected by N and _1/2 because of the effects of these constants on the initial n / p ratio. Before (electron) neutrino decoupling, this ratio is kept in thermal equilibrium by weak interactions so that

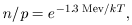
(7)

whereas afterwards the ratio is virtually frozen at the value given by (7) with T equal to the decoupling temperature T_d. Because the weak-interaction cross section is proportional to (energy)² or T², the reaction time scale varies as (n G_F² T²)^-1 or _1/2 T^-5, where n is the number density of electron neutrinos, whereas the expansion time scale is ~ (G )^-1/2 proportional to (11/4 + (7/8)N)^-1/2 T^-2, so the decoupling temperature varies as _1/2^1/3(11/4 + (7/8)N)^1/6. This means that larger values of _1/2 or N, lead to higher T_d and hence to larger n / p and larger primordial helium abundances. After decoupling, n / p decreases only slowly through free decay (and residual weak interactions) leading to a very slow dependence on given by

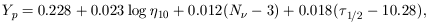
(8)

(Olive et al. 1990) for 2.5 ₁₀ 10 and with _1/2 in minutes. Recent experimental values of _1/2 are 10.25 (Mampe et al. 1989; Gudkov et al. 1990) and 10.32 (Byrne et al. 1990). The sensitivity to N, first noted by Hoyle & Tayler (1964), and the relatively high degree of precision to which Y_p can be estimated (see below), have enabled cosmological limits to be placed on the number of neutrino families, first no more than 5 (Steigman, Schramm & Gunn 1977), then 4 (Yang et al. 1984) and finally 3 (Pagel 1988; Pagel & Simonson 1989; Olive et al. 1990) which was confirmed in accelerator experiments on the Z^o (e.g. Ellis, Salati & Shaver 1990), but with the provisos that SBBN does not exclude neutrinos massive enough to be non-relativistic at a few Mev, which are excluded up to 45 Gev by Z^o decay, and conversely SBBN does exclude hypothetical light particles coupling to photons but not to the Z^o. Consistency of SBBN theory also imposes an upper limit on _1/2 of 10.4 minutes. Upper and lower limits to and _b0 h₀² resulting from a comparison of SBBN predictions with primordial abundances deduced by various means from observations, as discussed below, are shown by the tall vertical lines in fig. 1.