4.5. The primordial helium abundance

For whatever reason, the nitrogen regression gives a slightly better correlation than the oxygen one and a slightly more precise result, which is therefore the one that we currently adopt. Table 2 compares it with some previous estimates and it shows that, despite the various arguments raised in Section 4.3, the result has been remarkably stable for over a decade, during which time there have been larger changes in the estimates of the neutron half life (these have come down; see Tayler 1990) and the restriction to N = 3 has been confirmed in accelerator experiments. The systematic errors remaining in our estimates of Y_p are inevitably a matter of judgement. I see no reason why they should exceed the formal standard error of 0.004, in which case there is 95 per cent confidence that the true value does not exceed 0.240 as shown by the horizontal line in fig. 1 and Y_p gives the tightest upper limit to the density parameter . Specifically, assuming SBBN, ((D + ³He/H)_p 10^-4, _1/2 10.1 min and Y_p 0.240), the limits from equation (8) are

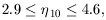
(15)

or, from equation (5),

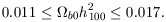
(16)

h₁₀₀ is universally agreed to be between 0.4 and 1.0; most probably it exceeds 0.7 (Tully 1990) which rules out an Einstein-de Sitter universe with = 1 because of the ages of globular clusters. If 0.7 h₁₀₀ 1.0 , then

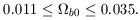
(17)

The lower limit calls for baryonic dark matter, since visible matter in spiral and irregular galaxies corresponds to _vis = 0.002h₁₀₀^-1 and the larger mass:light ratio found in ellipticals is itself probably due in large part to white dwarfs and neutron stars (Yoshii & Arimoto 1987).

Table 2. Estimates of primordial helium abundance with ±1 errors

.230 ± .004	Lequeux et al. 1979
<.243 ± .010	Kunth & Sargent 1983
.234 ± .008	Kunth & Sargent 1983 without II Zw 40
.232 ± .004	Peimbert 1985
.237 ± .005	Pagel, Terlevich & Melnick 1986
.232 ± .004	Pagel 1987a
.230 ± .006	Torres-Peimbert, Peimbert & Fierro 1989
.229 ± .004	Pagel & Simonson 1989

This amount of dark matter could be present in dark halos of spirals deduced from 21 cm rotation curves and the dynamics of the local group; alternatively, it might be there in the form of low surface-brightness galaxies not counted in conventional optical surveys (Pagel 1990). The upper limit less than most estimates of ₀ (total) around 0.2 based on galaxy cluster dynamics (Peebles 1986) leaving some space for non-baryonic dark matter.

In the inhomogeneous BBNS case, the corresponding limits are (rough

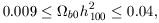
(18)

or with 0.7 h₁₀₀ 1.0

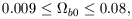
(19)

which leaves the case for dark baryornc matter virtually unchanged, but so what weakens that for non-baryonic matter (it would weaken it even more - possibly up to the point of extinction - if h₁₀₀ were smaller!). Whether inhomogeneous case actually applies is unclear; the physical question of extence of a first-order transition still remains to be settled, and then there is question of whether the primordial deuterium and helium abundances and neutron half-life can be squeezed tightly enough to cause real embarrassment to SBBN. Such would be the case, for example, if one could demonstrate exclusively that Y_p < 0.235, but there are enough opportunities for system ore than speculative errors in existing data to make this possibility no more than speculative the time being.

I thank the UK PATT for assigning time on the AAT for work description here and the Director and staff of the Anglo-Australian Observatory for will and expert assistance. I also thank Roberto Terlevich, Mike Edmunds and Simonson, all of whom played an essential part in our quest for more certain about primordial helium.