2.6. Spectrophotometric Flux Calibration
In this section, we will outline some of the important considerations for flux calibration of spectroscopic monitoring data, directed primarily towards ground-based optical observers.
In AGNs, aperture effects arise because the source is comprised of multiple components, some of which have angular structure on scales similar to the width of the point-spread function (PSF). The basic requirement for accurately flux-calibrating AGN spectra is that stable fractions of light from the AGN continuum source and BLR (both point-like at even the 0".01 level) and the NLR and the host galaxy (both extended even at arcsecond levels) must enter the aperture. We note that even in the case of space-based observations, there is a trade-off between aperture size and pointing uncertainty: the goal is to minimize the amount of host-galaxy starlight entering the aperture (arguing for a smaller aperture), while ensuring that the amount of admitted starlight is constant (arguing for an aperture large relative to the pointing accuracy of the telescope). In the UV, however, this is a less-significant problem because the host galaxy is so much fainter than the AGN itself.
Mitigation of aperture effects is one of the most important considerations for a ground-based monitoring program. This is important to keep in mind, as most AGN observers are used to background-limited observations of point sources, and this calls for adjusting the slit width for variations in seeing in order to optimize the S/N of the data. However, this is exactly the wrong thing to do if you are monitoring Seyfert galaxy variations, since calibration accuracy is almost always determined by systematics rather than photon statistics. Most observers do know that you need to open up the aperture for absolute spectrophotometry, however, and this is precisely what needs to be done in monitoring programs, as we will explain below.
The standard method of absolute flux calibration is to determine from observations of spectrophotometric standard stars how counts per second per pixel on the detector translates to flux per unit wavelength. However, standard absolute spectrophotometry is far too inaccurate for ground-based AGN monitoring; the typical accuracy that can be achieved on photometric nights is about 5%. Furthermore, at most observing sites, only a relatively small fraction of nights are of sufficient quality and stability for absolute spectrophotometry to be useful. Even at a good site like Kitt Peak, fewer than 1/3 of the nights are photometric. However, more than 2/3 of all nights (including bright time) are good enough to get quality spectra of bright AGNs with a 1-2-m telescope with a typical photometric accuracy about 15%. Since we need a high rate of sampling and do not wish to discard more than half of the potentially usable nights, secondary higher-accuracy calibration methods must be used. In ground-based AGN monitoring, there are two commonly used high-accuracy flux-calibration methods, which we outline below:
4959, 5007 doublet is excellent for
this method because these lines are strong, relatively unblended, and
close in wavelength to H
and
4686. Unlike the broad
lines, the narrow lines are almost always expected to be constant
in flux. The light-crossing time for the NLR is
large (typically 100-1000 years) as is the
recombination time (about 100 years; see Eq. (17)
in Sec. 3),
so any short-term variability is smeared out.
This method also has limitations:
(a) most narrow lines are blended and/or weak,
(b) the method works best at reasonably high spectral resolution,
when the narrow-lines are at least partially resolved,
and (c) in nearby AGNs, the NLR is often extended on scales of
arcseconds, which introduces the possibility of aperture effects.
The last of these problems deserves serious consideration. If the NLR is extended, measuring a consistent flux is difficult due to aperture effects, as described above; either centering and guiding errors or differences in the seeing between observations can alter the calibration of the spectrum. However, it is possible to understand the nature of these effects so that in principle one can correct for them, or at minimum one can pursue mitigation strategies to reduce their influence. To do this, one must know (a) the surface brightness distributions of the extended components (the host galaxy and the NLR) and (b) the PSF, including the seeing component, for the instrument at the time of the observations.
With a good model for the surface brightness distributions, we can still use the narrow-lines for flux calibration, and then apply a seeing-dependent flux correction 89, 68. Even if the seeing is not measured, such models can be used to give us an idea of how badly our observations might be adversely affected by seeing variations. As an example, the corrections to the point-source fluxes (broad lines and AGN continuum) and host galaxy flux that need to be applied in the case of NGC 4151 are shown in Fig. 5 for different aperture geometries. We can readily conclude from these diagrams that seeing-dependence of the correction factors is smaller for larger apertures, as can be expected intuitively. A useful generalization is that the corrections for seeing effects are generally not necessary if the aperture in both dimensions is larger than the worst seeing, as measured by the full-width at half-maximum (FWHM) of a stellar image.
|
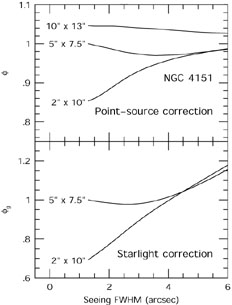
Figure 5. Aperture corrections (as defined
by Peterson et al.
68)
for NGC 4151. These are multiplicative adjustments
that must be made to (a) the broad emission-line and
AGN continuum fluxes (top panel) and (b) the host-galaxy
starlight contribution (bottom panel) as a function of
seeing when the spectra are calibrated by assuming a
constant flux in [O III]
|