4.5. Uncertainties in Cross-Correlation Lags

Although cross-correlation techniques have been applied to AGN time series for about 15 years, there is still no obvious or even universally agreed-upon way to assess the uncertainties in the lag measurements obtained. At present, the most effective technique seems to be a model-independent Monte-Carlo method known as FR/RSS (for "flux redistribution/random subset selection") ⁷⁰ .

FR/RSS is based on a computationally intensive statistical method known as a "bootstrap". The bootstrap works as follows: suppose that you have a set of N data pairs (x_i, y_i) and that linear regression yields a correlation coefficient r. How accurate is r? In particular, how sensitive is it to the influence of individual points? One can assess this by a Monte Carlo process where one selects at random N points from the original sample, without regard to whether or not any point has been selected previously. For the new sample of N points (some of which are redundant selections from the original sample, while some points in the original sample are missing), the linear correlation coefficient is recalculated. When this is done many times, a distribution in r is constructed, and from this, one can assign a meaningful statistical uncertainty to the original experimental value of r.

This process can also be assigned to time series, except that the time tags of the points have to be preserved. In effect, then, this means that redundant selections are overlooked; the probability that in N selections of N points a point will be selected zero times is 1 / e, so the new time series, selected at random, has typically fewer points by a factor of 1 / e (hence the name "random subset selection"). Welsh ⁹² suggests that this should be modified in the sense that the weighting of each selected point should be proportional to sqrt[n_i], where n_i is the number of times the data point (x_i, y_i) is selected in a single realization. This is closer in philosophy to the original bootstrap, but it has not been rigorously tested yet.

The other part of the process, "flux redistribution," consists of changing the actual observed fluxes in a way that is consistent with the measured uncertainties. Each flux is modified by a random Gaussian deviate based on the quoted error for that datum (i.e., after a large number of similar modifications, the distribution of flux values would be a Gaussian with mean equal to the data value and standard deviation equal to the quoted error).

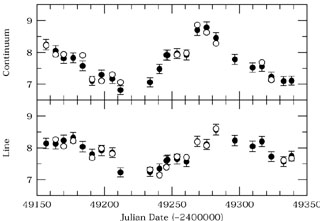
Figure 29. The filled circles show the Mrk 335 light curve from Fig. 23, but now with error bars shown. The open circles show a single FR/RSS Monte Carlo realization; the points are selected from the total subset at random, and the fluxes are adjusted as Gaussian deviates. Note that some of the original data points are not seen because the selected flux-adjusted points cover them. The realization shown here gives cent = 17.9 days, compared to cent = 15.6 days for the whole data set.

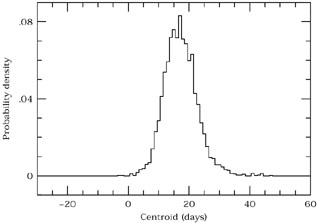
A single sample FR/RSS realization is shown schematically in Fig. 29. For each such realization, a cross-correlation is performed and the centroid is measured. A large number of similar realizations will produce a "cross-correlation peak distribution" (CCPD) ⁴⁹ , as shown in Fig. 30. The CCPD can be integrated to assign formal uncertainties (usually ± 1) to the value of _cent measured from the entire data set.

Figure 30. Multiple Monte-Carlo realizations such as those in Fig. 29 are used to build up a cross-correlation peak distribution (CCPD). Relative to the measured CCF centroid for the whole data set ( = 15.6 days), the ± 1 width of this distribution is +7.2, -3.1 days.