2. COSMOLOGICAL PARAMETERS AND OBSERVATIONS ON LARGE SCALES

The table below ⁽²⁾ summarizes the current observational information about the cosmological parameters, with estimated 1 errors. The quantities in brackets have been deduced using at least some of the CDM assumptions. Is is apparent that there is impressive agreement between the values of the parameters determined by various methods, including those based on CDM. In particular, (A) several different approaches (some of which are discussed further below) all suggest that _m 0.3; (B) the location of the first acoustic peak in the CMB angular anisotropy power spectrum, now very well determined independently by the BOOMERANG [17] and MAXIMA1 [18] balloon data [19, 20] and by the DASI interferometer at the South Pole [21], implies that _m + 1; and (C) the data on supernovae of Type Ia (SNIa) at redshifts z = 0.4 - 1.2 from two independent groups imply that - 4/3 1/3. Any two of these three results then imply that 0.7. The 1 errors in these determinations are about 0.1.

Questions have been raised about the reliability of the high-redshift SNIa results, especially the possibilities that the SNIa properties at high redshift might not be sufficiently similar to those nearby to use them as standard candles, and that there might be "grey" dust (which would make the SNIa dimmer but not change their colors). Although the available evidence disfavors these possibilities, ⁽³⁾ additional observations are needed on SNIa at high redshift, both to control systematic effects and to see whether the dark energy is just a cosmological constant or is perhaps instead changing with redshift as expected in "quintessence" models [3]. Such data could be obtained by the proposed SuperNova Acceleration Probe (SNAP) satellite [23], whose Gigapixel optical camera and other instruments would also produce much other useful data. But it is important to appreciate that, independently of (C) SNIa, (A) cluster and other evidence for _m 0.3, together with (B) ~ 1° CMB evidence for _m + 1, imply that 0.7.

Table 1. Cosmological Parameters [results assuming CDM in brackets]

All methods for determining the Hubble parameter now give compatible results, confirming our confidence that this crucial parameter has now been measured robustly to a 1 accuracy of about 10%. The final result [24] from the Hubble Key Project on the Extragalactic Distance Scale is 72& #177; 8 km s^-1 Mpc^-1, or h = 0.72 ± 0.08, where the stated error is dominated by one systematic uncertainty, the distance to the Large Magellanic Cloud (used to calibrate the Cepheid period-luminosity relationship). The most accurate of the direct methods for measuring distances d to distant objects, giving the Hubble parameter directly as H₀ = d /v where the velocity is determined by the redshift, are (1) time delays between luminosity variations in different gravitationally lensed images of distant quasars, giving h 0.65, and (2) the Sunyaev-Zel'dovich effect (Compton scattering of the CMB by the hot electrons in clusters of galaxies), giving h 0.63 [25, 24]. For the rest of this article, I will take h = 0.7 whenever I need to use an explicit value, and express results in terms of h₇₀ H₀/70 km s^-1 Mpc^-1.

For a CDM universe with _m = (0.2)0.3(0.4, 0.5), the expansion age is t₀ = (15.0)13.47(12.41, 11.61) h₇₀^-1 Gyr. Thus for _m 0.3 - 0.4 and h 0.7, there is excellent agreement with the latest estimates of the ages of the oldest globular cluster stars in the Milky Way, both from their Main Sequence turnoff luminosities [26], giving 12 - 13 ± 2 Gyr, and using the thorium and uranium radioactive decay chronometers [27], giving 14 ± 3 Gyr and 12.5 ± 3 Gyr, respectively.

The simplest and clearest argument that _m 1/3 comes from comparing the baryon abundance in clusters f_b M_b/M_tot to that in the universe as a whole _b / _m, as emphasized by White et al. [28]. Since clusters are evidently formed from the gravitational collapse of a region of radius ~ 10 Mpc, they should represent a fair sample of both baryons and dark matter. This is confirmed in CDM simulations [29]. The fair sample hypothesis implies that

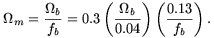
(1)

We can use this to determine _m using the baryon abundance _b h² = 0.019 ± 0.0024 (95% C.L.) from the measurement of the deuterium abundance in high-redshift Lyman limit systems [30, 31]. Using X-ray data from an X-ray flux limited sample of clusters to estimate the baryon fraction f_b = 0.075h^-3/2 gives [32] _m = 0.25h^-1/2 = 0.3 ± 0.1 (using h = 0.70 ± 0.08). Estimating the baryon fraction using Sunyaev-Zel'dovich measurements of a sample of 18 clusters gives f_b = 0.077h^-1 [25], and implies _m = 0.25h^-1 = 0.36 ± 0.1.

There is another way to use clusters to measure _m, which takes advantage of the fact that the redshift at which structures form depends strongly on _m. This happens because in a low-density universe the growth rate of fluctuations slows when, on the right hand side of the Friedmann equation,

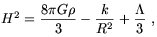
(2)

the first (matter) term becomes smaller than either the second (curvature) term (for the case of an open universe) or the third (cosmological constant) term. As I have already discussed, the term appears to be dominant now; note that if we evaluate the Friedmann equation at the present epoch and divide both sides by H₀², the resulting equation is just

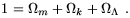
(3)

Therefore, if we normalize the fluctuation power spectrum P(k) for an _m = 1 (Einstein-de Sitter) cosmology and for a CDM one by choosing ₈ so that each is consistent with COBE and has the same abundance of clusters today, then at higher redshifts the low-_m universe will have a higher comoving number density of clusters. Probably the most reliable way of comparing clusters nearby with those at higher redshift uses the cluster X-ray temperatures; the latest results, comparing 14 clusters at an average redshift of 0.38 with 25 nearby clusters, give _m = 0.44 ± 0.12 [33, 34]. There is greater leverage in this test if one can use higher redshift clusters, but the challenge is to find large samples with well understood cluster selection and properties. The largest such sample now available is from the Las Companas Distant Cluster Survey, which goes to redshifts ~ 1, from which the preliminary result is _m = 0.30 ± 0.12 (90% CL) [35].

² Further discussion and references are given in [16]. Back.

³ For example, SNIa at z = 1.2 and ~ 1.7 apparently have the brightness expected in a CDM cosmology but are brighter than would be expected with grey dust, and the infrared brightness of a nearer SNIa is also inconsistent with grey dust [22]. Back.