3. FURTHER SUCCESSES OF CDM

We have already seen that CDM correctly predicts the abundances of clusters nearby and at z 1 within the current uncertainties in the values of the parameters. It is even consistent with P(k) from the Ly forest [36] and from CMB anisotropies. Low-_m CDM predicts that the amplitude of the power spectrum P(k) is rather large for k 0.02h / Mpc^-1, i.e. on size scales larger (k smaller) than the peak in P(k). The largest-scale surveys, 2dF and SDSS, should be able to measure P(k) on these scales and test this crucial prediction soon; preliminary results are encouraging [37].

The hierarchical structure formation which is inherent in CDM already explains why most stars are in big galaxies like the Milky Way [14]: smaller galaxies merge to form these larger ones, but the gas in still larger structures takes too long to cool to form still larger galaxies, so these larger structures - the largest bound systems in the universe - become groups and clusters instead of galaxies.

What about the more detailed predictions of CDM, for example on the spatial distribution of galaxies. On large scales, there appears to be a pretty good match. In order to investigate such questions quantitatively on the smaller scales where the best data is available it is essential to do N-body simulations, since the mass fluctuations / are nonlinear on the few-Mpc scales that are relevant. My colleagues and I were initially concerned that CDM would fail this test, [38] since the dark matter power spectrum P_dm(k) in CDM, and its Fourier transform the correlation function (r), are seriously in disagreement with the galaxy data P_g(k) and _g(r). One way of describing this is to say that scale-dependent antibiasing is required for CDM to agree with observations. That is, the bias parameter b(r) [_g(r) / (r)]^1/2, which is about unity on large scales, must decrease to less than 1/2 on scales of a few Mpc [38, 39]. This was the opposite of what was expected: galaxies were generally thought to be more correlated than the dark matter on small scales. However, when it became possible to do simulations of sufficiently high resolution to identify the dark matter halos that would host visible galaxies [40, 41], it turned out that their correlation function is essentially identical with that of observed galaxies! This is illustrated in Fig. 1.

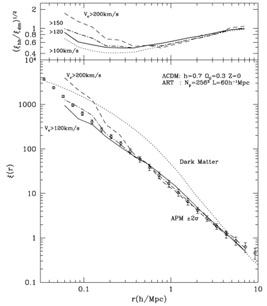
Figure 1. Bottom panel: Comparison of the halo correlation function in an CDM simulation with the correlation function of the APM galaxies [42]. The dotted curve shows the dark matter correlation function. Results for halos with maximum circular velocity larger than 120km s-1, 150km s-1, and 200km s-1 are presented by the solid, dot-dashed, and dashed curves, respectively. Note that at scales 0.3h-1Mpc the halo correlation function does not depend on the limit in the maximum circular velocity. Top panel: Dependence of bias on scale and maximum circular velocity. The curve labeling is the same as in the bottom panel, except that the dotted curve now represents the bias of halos with Vmax > 100km s-1. From Colin et al. [41].

Jim Peebles, who largely initiated the study of galaxy correlations and first showed that _g(r) (r / r₀)^-1.8 with r₀ 5h^-1Mpc [48], thought that this simple power law must be telling us something fundamental about cosmology. However, it now appears that the power law _g arises because of a coincidence - an interplay between the non-power-law _dm(r) (see Fig. 1) and the decreasing survival probability of dark matter halos in dense regions because of their destruction and merging. But the essential lesson is that CDM correctly predicts the observed _g(r).

The same theory also predicts the number density of galaxies. Using the observed correlations between galaxy luminosity and internal velocity, known as the Tully-Fisher and Faber-Jackson relations for spiral and elliptical galaxies respectively, it is possible to convert observed galaxy luminosity functions into approximate galaxy velocity functions, which describe the number of galaxies per unit volume as a function of their internal velocity. The velocity function of dark matter halos is robustly predicted by N-body simulations for CDM-type theories, but to connect it with the observed internal velocities of bright galaxies it is necessary to correct for the infall of the baryons in these galaxies [43, 44, 45], which must have happened to create their bright centers and disks. When we did this it appeared that CDM with _m = 0.3 predicts perhaps too many dark halos compared with the number of observed galaxies with internal rotation velocities V 200km s^-1 [46, 47]. While the latest results from the big surveys now underway appear to be in better agreement with these CDM predictions [49, 50], this is an important issue that is being investigated in detail [51].

The problem just mentioned of accounting for baryonic infall is just one example of the hydrodynamical phenomena that must be taken into account in order to make realistic predictions of galaxy properties in cosmological theories. Unfortunately, the crucial processes of especially star formation and supernova feedback are not yet well enough understood to allow reliable calculations. Therefore, rather than trying to understand galaxy formation from full-scale hydrodynamic simulations (for example [52]), more progress has been made via the simpler approach of semi-analytic modelling of galaxy formation (initiated by White and Frenk [53, 54, 55], recently reviewed and extended by Rachel Somerville and me [56]). The computational efficiency of SAMs permits detailed exploration of the effects of the cosmological parameters, as well as the parameters that control star formation and supernova feedback. We have shown [56] that both flat and open CDM-type models with _m = 0.3 - 0.5 predict galaxy luminosity functions and Tully-Fisher relations that are in good agreement with observations. Including the effects of (proto-)galaxy interactions at high redshift in SAMs allows us to account for the observed properties of high-redshift galaxies, but only for _m 0.3 - 0.5 [57]. Models with _m = 1 and realistic power spectra produce far too few galaxies at high redshift, essentially because of the fluctuation growth rate argument mentioned above.

In order to tell whether CDM accounts in detail for galaxy properties, it is essential to model the dark halos accurately. The Navarro-Frenk-White (NFW) [58] density profile _NFW(r) r^-1(r + r_s)^-2 is a good representation of typical dark matter halos of galactic mass, except possibly in their very centers (Section 4). Comparing simulations of the same halo with numbers of particles ranging from ~ 10³ to ~ 10⁶, my colleagues and I have also shown [59] that r_s, the radius where the log-slope is -2, can be determined accurately for halos with as few as ~ 10³ particles. Based on a study of thousands of halos at many redshifts in an Adaptive Refinement Tree (ART) [60] simulation of the CDM cosmology, we [61] found that the concentration c_vir R_vir / r_s has a log-normal distribution, with 1 (log c_vir) = 0.14 at a given mass [62, 63]. This scatter in concentration results in a scatter in maximum rotation velocities of V_max / V_max = 0.12; thus the distribution of halo concentrations has as large an effect on galaxy rotation curves shapes as the well-known log-normal distribution of halo spin parameters . Frank van den Bosch [64] showed, based on a semi-analytic model for galaxy formation including the NFW profile and supernova feedback, that the spread in mainly results in movement along the Tully-Fisher line, while the spread in concentration results in dispersion perpendicular to the Tully-Fisher relation. Remarkably, he found that the dispersion in CDM halo concentrations produces a Tully-Fisher dispersion that is consistent with the observed one. ⁽⁴⁾

⁴ Actually, this was the case with the dispersion in concentration (log c_vir) = 0.1 found for relaxed halos by Jing [62], while we [61] found the larger dispersion mentioned above. However Risa Wechsler, in her dissertation research with me [63], found that the dispersion in the concentration at fixed mass of the halos that have not had a major merger since redshift z = 2 (and could thus host a spiral galaxy) is consistent with that found by Jing. We also found that the median and dispersion of halo concentration as a function of mass and redshift are explained by the spread in halo mass accretion histories. Back.