Copyright © 1998 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1998. 36:
267-316 Copyright © 1998 by Annual Reviews. All rights reserved |
2.2. Low Resolution Spectroscopy: Mean Absorption
The most basic observable of the
Ly forest
is the quantity originally sought by
Gunn and Peterson (1965),
the flux decrement D, or the mean fraction of the QSO continuum
absorbed. It has become standard practice to
measure the mean flux decrement DA between the
Ly
forest
is the quantity originally sought by
Gunn and Peterson (1965),
the flux decrement D, or the mean fraction of the QSO continuum
absorbed. It has become standard practice to
measure the mean flux decrement DA between the
Ly and
Ly
and
Ly emission lines
(Oke & Korycansky
1982):
emission lines
(Oke & Korycansky
1982):
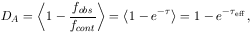
| (1) |
where fobs is the observed (= residual) flux,
fcont the
estimated flux of the unabsorbed continuum, and
 is the resonance
line optical depth as a function of wavelength or redshift. The
absorption is measured against a continuum level usually taken to be a
power law in wavelength extrapolated from the region redward of the
Ly
is the resonance
line optical depth as a function of wavelength or redshift. The
absorption is measured against a continuum level usually taken to be a
power law in wavelength extrapolated from the region redward of the
Ly emission line. A
knowledge of the mean absorption allows us, for example,
to determine the resulting broadband color
gradients in a QSO or high redshift galaxy spectrum, as caused by
the Ly
emission line. A
knowledge of the mean absorption allows us, for example,
to determine the resulting broadband color
gradients in a QSO or high redshift galaxy spectrum, as caused by
the Ly forest. Measurements
of DA from large datasets were performed by (among
others)
Oke & Korycansky
(1982),
Bechtold et al. (1984),
O`Brian et al (1988),
Steidel & Sargent
(1987),
Giallongo & Cristiani
(1990),
Dobrzycki & Bechtold
(1991),
Schneider et al (1991,
and refs. therein). Obviously, at the price of getting only one
number out of each QSO spectrum, this technique gives the most
model-independent measurement possible.
forest. Measurements
of DA from large datasets were performed by (among
others)
Oke & Korycansky
(1982),
Bechtold et al. (1984),
O`Brian et al (1988),
Steidel & Sargent
(1987),
Giallongo & Cristiani
(1990),
Dobrzycki & Bechtold
(1991),
Schneider et al (1991,
and refs. therein). Obviously, at the price of getting only one
number out of each QSO spectrum, this technique gives the most
model-independent measurement possible.
With DA measurements available over a range of
redshifts the redshift
evolution of the Ly forest
can be investigated. Here the concept of an effective optical depth
forest
can be investigated. Here the concept of an effective optical depth
 eff(z), as
defined in Equation (1) becomes useful.
If we characterize a Ly
eff(z), as
defined in Equation (1) becomes useful.
If we characterize a Ly forest as a random distribution of
absorption systems in column density N, Doppler parameter
b, and
redshift z space, such that the number of lines per interval
dN, db and dz is given by
forest as a random distribution of
absorption systems in column density N, Doppler parameter
b, and
redshift z space, such that the number of lines per interval
dN, db and dz is given by
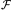 (N, b,
z)dN db dz, then
(N, b,
z)dN db dz, then
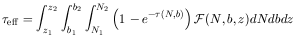
| (2) |
(Paresce et al 1980),
for a population of absorbers without spatial or velocity correlations.
Assuming that the N and b distribution functions are
independent of redshift,
and the redshift evolution of the number density of lines can be
approximated by a power law, we can write
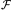 (N, b,
z) = (1 +
z)
(N, b,
z) = (1 +
z) F(N, b), and
F(N, b), and
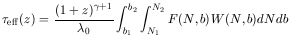
| (3) |
where the rest frame equivalent width is given by
W = (1 + z)-1
 0-1
0-1
 d
d (1 -
e-
(1 -
e- ).
).
This relation enables us to measure the redshift evolution of the
number density of Ly forest
clouds,
d
forest
clouds,
d / dz
/ dz
 (1 +
z)
(1 +
z) , from
the redshift dependence of the effective
optical depth (
, from
the redshift dependence of the effective
optical depth ( eff
eff
 (1 +
z)
(1 +
z) +1)
even if we do not resolve the individual absorption lines
(Young et al 1982b;
Jenkins & Ostriker
1991;
Zuo 1993;
Press et al 1993;
Lu & Zuo 1994).
The results of this approach are discussed below in the section
on Ly
+1)
even if we do not resolve the individual absorption lines
(Young et al 1982b;
Jenkins & Ostriker
1991;
Zuo 1993;
Press et al 1993;
Lu & Zuo 1994).
The results of this approach are discussed below in the section
on Ly forest evolution,
together with the conclusions from line counting methods.
forest evolution,
together with the conclusions from line counting methods.
The largest uncertainties in D or
 eff are probably
caused by our ignorance
about the precise QSO continuum level, against which the absorption is
measured. Additional errors stem from the amount of
absorption contributed by metal lines, which often cannot
be identified as such and then removed from low resolution
Ly
eff are probably
caused by our ignorance
about the precise QSO continuum level, against which the absorption is
measured. Additional errors stem from the amount of
absorption contributed by metal lines, which often cannot
be identified as such and then removed from low resolution
Ly spectra.
spectra.