Annu. Rev. Astron. Astrophys. 1998. 36: 267-316 Copyright © 1998 by Annual Reviews. All rights reserved

2.3. Intermediate Resolution Spectroscopy: Line Counting

At higher resolution, where it becomes possible to distinguish between discrete absorption lines, the distribution of the lines in terms of equivalent width W and redshift z is the next most sophisticated tool. Just as the mean absorption D under certain conditions provides a measure of the mean (gas) density of the universe, so does the number of lines per unit equivalent width, d²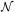 / dW dz essentially measure the clumpiness of the Ly forest gas. An exponential distribution in W and a power law dependence on (1 + z) have been found to provide a reasonable match to the observed line counts (Sargent et al (1980); Young et al (1982b); Murdoch et al (1986)). For lines above a rest equivalent width threshold W > 0.16 Å,

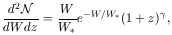
(4)

with a typical W_* 0.27 Å (Bechtold 1994), and 1.5 < < 3 (see also the discussion on redshift evolution below). The multiplicative form of Equation (4) is justified by a relatively weak dependence of W_* on z (Murdoch et al 1986). The exponential model fits less well for lines with W < 0.3 Å as the weaker lines are moving off the saturated part of the curve of growth and become more numerous.

Unfortunately, statistics involving the observed equivalent width distribution are not easy to interpret in physical terms. The W values are usually obtained by simply measuring statistically significant downward excursions from the QSO continuum. Without properly deblending the lines (impossible at low resolution) the curve of growth cannot be used to relate W to the more meaningful parameters N and b.