Annu. Rev. Astron. Astrophys. 1998. 36: 267-316 Copyright © 1998 by Annual Reviews. All rights reserved

5.1. Hydrodynamic Simulations of the Ly Forest

NUMERICAL APPROACHES     From the early 1990s on hydrodynamic cosmological simulations became sufficiently realistic to be able to quantitatively predict the physical properties of the intergalactic medium and the high redshift Ly forest from the initial conditions of a given structure formation model (e.g., Cen & Ostriker 1993). A Ly forest spectrum is completely specifed by the Hubble constant, gas density, temperature, peculiar velocity, and neutral fraction along the LOS. By predicting these quantities for artificial QSO LOS through simulated slices of the universe it becomes possible to examine the correspondence between Ly forest absorbers and the physical properties of the underlying gaseous structures. This approach was first taken by Cen et al 1994 (see also Miralda-Escudé et al 1996) using an Eulerian hydro-simulation of a CDM model. Since then a range of other numerical techniques have been applied to different cosmological models. The basic properties of the Ly forest turn out to be only weakly dependent on the cosmological model, and similar answers have been obtained with a variety of approaches: Petitjean et al (1995) grafted the baryons onto a COBE normalized cold dark matter distribution from an DM particle mesh simulation, using an analytic prescription to track the thermal history of the gas. A standard CDM model has been studied by Zhang et al (1995, 1997) with an Eulerian code, and by Hernquist et al (1996), with a Lagrangian, Smoothed Particle Hydrodynamics (SPH) technique. As a crude general rule of thumb the Eulerian codes are capable of higher resolution for the void regions producing the lowest column density Ly forest, whereas the Lagrangian codes are superior for regions like minihalos or galaxies where a larger dynamic range is required. Thus the use of SPH codes has been extended to study damped Ly systems (Katz et al 1996) and metal absorption systems (Haehnelt et al 1996a). Hybrid schemes (e.g., Wadsley & Bond 1997) can be tailored to capture the influence of both, large scale (long wavelength) gravitational effects and the small scale gas dynamics, on the formation of Ly absorbers.

THE NATURE OF LYMAN ALPHA ABSORBERS     Inspite of some quantitative differences a generic picture of the Ly forest has emerged from these studies: Low column density systems (log N(HI) 14) are associated with sheet-like structures, not unlike small versions (length scale ~ a few hundred kpc to 1 Mpc proper) of Zeldovich pancakes. Gas accretes through weak shocks (creating a double humped temperature profile), and settles in a dense, central cooling layer, presumably to form stars. At the lowest column densities gas remains unshocked and just bounces back because of the hydrostatic pressure. The gas is partly confined by gravity and partly by ram-pressure. Higher column density clouds arise in more filamentary structures, with column density contours of log N(HI) ~ 14 extending continously and with relatively constant thickness (~ 40 - 100 kpc proper) over Mpc distances. With increasing column density the absorber geometry becomes rounder; column density contours at log N(HI) 16 invariably are spherical, entering the regime where the absorbers more closely correspond to minihalos; there the enclosed gas column is high enough to make the absorption system appear as a Lyman limit or damped Ly system. Figure 2 shows the spatial appearance of the Ly absorbers. The visual appearance of the low column density, sheetlike-filamentary structure has been aptly described as a "Cosmic Web" (Bond & Wadsley 1997). Looking at the higher column density, optically thick gas on scales of several Mpcs one gets a somewhat different impression of chains of mini- or larger halos, lining up like pearls on a string, quite similar to the structure seen in N-body simulations of the dark matter distribution. Confirming earlier analytical work, a large fraction of all baryons (80 - 90%) resides in the low column density Ly forest, mostly in the column density range 14 < log N(HI) < 15.5 (Miralda-Escudé et al 1996).

Figure 2. HI column density contours for a slice of the 10 h-1 Mpc (comoving) box from the CDM simulation by Miralda-Escudé et al (1996).

A glance at a typical density-temperature diagram (Figure 3) for random lines of sight through one of the SPH simulations (Haehnelt et al 1996b) reveals significant departures from thermal photoionization equilibrium for all but the highest density gas (n_H < 10^-3cm^-2). The temperature density relation is generally steeper than the equilibrium curve, because the lower density gas cools by expansion, while the gas in the density range n_H ~ a few times 10^-5 - 10^-3 cm^-3 is heated by adiabatic compression or shock heating. Temperatures below 10⁴K occur in voids where the expansion velocity is largest.

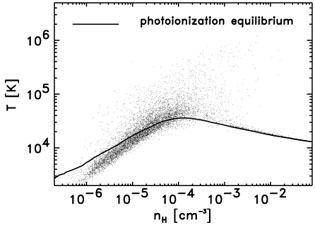
Figure 3. Density - temperature (n - T) diagram of the Ly forest at redshift 3.1 from an SPH simulation of a standard CDM universe (Haehnelt et al 1996b). Each dot represents the mean values of the total hydrogen density n and the gas temperature T along a random line of sight through the simulated box. The solid curve gives the locus of thermal photoionization equilibrium. Departures from this curve are due to the dynamical nature of the universe. For all but the most dense regions expansion cooling in voids (low density regions) and heating by compression and shocks during gravitational collapse steepen the T(n) relation compared to the equilibrium curve.

The gas is still being accreted at the epoch of observations (z ~ 3). Nevertheless, the lower column density flattened gas structures expand in proper coordinates because the gravitational pull decreases together with the dark matter surface density, as the universe expands. Many of the weaker absorption lines arise in low density, relatively extended regions, which expand with a substantial fraction of the Hubble velocity. The expansion, and the low temperatures due to the low density and the adiabatic cooling in voids ensure that at column densities (log N(HI) 13) bulk motion becomes the dominant source of line broadening (Miralda-Escudé et al 1996; Weinberg et al 1997).

MATCHING THE OBSERVATIONS     The simulations have been quite successful in matching the overall observed properties of the absorption systems, and the agreement ranges from the acceptable to the amazing. The shape of the column density distribution and the Doppler parameter distribution are reasonably well reproduced by the simulations. (Cen et al 1994; Zhang et al 1995, 1997; Hernquist et al 1996; Miralda-Escudé et al 1996). Although the approximate range of Doppler parameters is hard to miss (with photoionization being the great equalizer), subtle effects can raise or lower the mean line width by ~ 30% and change the shape of the Doppler parameter distribution. There may be some discrepancy for the Doppler parameters between different simulations (Zhang et al 1997, Davé et al 1997, Miralda-Escudé et al 1996) but it is not yet clear whether this is due to different types of data analysis, different assumptions about the process of reionization, or limited numerical resolution. A departure from Voigt profile shapes, especially the broad wings of weak lines signifying bulk motion broadening in sheets, is seen in the simulations (Cen et al 1994) and appears to be present in real high resolution spectra (Rauch 1996). The large transverse sizes of the absorbers seen against background QSO pairs and lensed QSOs are readily explained by the coherence length of the sheets and filaments (Miralda-Escudé et al 1996; Charlton et al. 1997; Cen & Simcoe 1997). The weak clustering amplitude appears to be in agreement with the observations. The histogram of residual fluxes in the Ly forest is reproduced very well by the models (Rauch et al 1997). Conversely, we may take this as observational evidence in favor of some sort of hierarchical structure formation model.

The evolution of the Ly forest with time at high redshift is mainly driven by the Hubble expansion and the resulting increase in the mean ionization of the gas, and to a lesser degree by the gas streaming along the filaments (Miralda-Escudé et al 1996). Muecket et al (1996), from their simulation, find that the number of absorbers per redshift is given by a broken power law, with ~ 2.6 (1.5 < z < 3) and ~ 0.6 (0 < z < 1.5), (log N(HI) > 14) (Riediger et al 1998), a remarkable agreement with the observed data. The break in the power law can be understood as a change with time in the dimensionality of the structures dominating the absorption. The sheetlike absorbers dominating the high redshift Ly forest are expanding with time and are dropping below the detection threshold first because of their low column density, leaving the absorption from the less rapidly evolving gas distribution in the filaments and knots to dominate. There the column density also decreases, but since the original column was higher, the filaments remain visible for longer. Continuing infall also contributes to the increasing prominence of the more compact structures.