Annu. Rev. Astron. Astrophys. 1998. 36: 267-316 Copyright © 1998 by Annual Reviews. All rights reserved

5.2. The Ly Forest as a Cosmological Laboratory

The first generation of simulations was largely aimed at establishing the physical properties of the Ly absorbers. The newly gained understanding of the nature of the Ly forest and the increasing realism of the simulations, together with new semi-analytic methods and novel ways of data analysis have brought quantitative cosmology with the low column density Ly forest within reach.

Aside from the cosmic microwave background, the intergalactic medium is the only astrophysical environment for which observable properties can (at least in principle) be calculated from a simple set of cosmological initial conditions. This is because at z~ 3 the density fluctuations = / 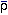- 1 on spatial scales relevant for detectable Ly lines (on the order of 10² kpc comoving) are not too far into the non-linear regime, so the history of the gas causing most of the low column density Ly forest has not yet been obliterated by virialization and dissipative processes. Overdensities between 0 and ~ 15 roughly correspond to Ly lines on the linear part of the curve of growth (12 log N 14), where spectroscopic measurements are most sensitive. When observing structures still dominated by gravity the problem of "bias", one of the main obstacles to doing cosmology with galaxies, largely can be avoided.

The link between the observable appearance of the Ly forest and the various cosmological input parameters can be described by the Gunn-Peterson relation for the HI optical depth, generalized to include an inhomogenous density and velocity field. As long as the gas is highly ionized and in photoionization equilibrium (not necessarily thermal equilibrium), and the gas is unshocked, the optical depth is given by

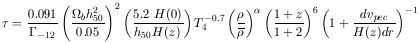
(17)

This equation relates the optical depth for Ly absorption to the mean baryonic density (in gas) in units of the critical density, _b, the Hubble constant at redshift z, H(z), the average gas temperature T, the proper baryon density , the photoionization rate _-12 in units of 10 ^-12 s^-1, and the gradient of the local peculiar velocity dv_pec/dr along the LOS. A further convolution with a Voigt profile is necessary to include the proper thermal velocity broadening. To turn this relation into a complete description of the observed Ly forest, cosmology has to predict the cosmic density and velocity fields, the fraction of the closure density in the form of gas, the equation of state, T = T(), and the ionizing radiation field. The exponent (=2 for an isothermal gas) takes account of the fact that in denser regions of the universe the gas is typically warmer because it is more effectively heated by photoionization, but also depends on the reionization history of the gas and the amount of adiabatic expansion/compression. Hui & Gnedin (1997), and Croft et al (1997a) find values of 1.6 - 1.8.

Cosmological parameters can now be "measured" by iterating simulations with different input parameters until the simulated statistics of (z) (the mean absorption, correlation function etc) match the observed ones. Perhaps the simplest cosmological parameter combination to be obtained is related to the baryon density, _b. Given eqn. (17) the optical depth scales approximately with ( h₅₀²) / _-12. Using an independent estimate of the photoionization rate _-12, e.g., from the integrated UV radiation of QSOs, one can determine _b.

The simulations show that a rather high _b h² is required to reproduce the amount of observed absorption, even for a conservatively low estimate of (Hernquist et al 1996, Miralda-Escudé et al 1996). If the ionizing background is given by the known QSOs alone and a Haardt & Madau (1996) spectrum (scaled to J_-21 0.23, at z = 2) is adopted, _b h² > 0.017 (Rauch et al 1997). Although the observations of _eff on which the result is based, are still somewhat uncertain, relatively large _b values appear to be an inherent feature of hierarchical structure formation and cannot be avoided unless most of the low column density absorption dominating the Ly forest has a different physical origin (Weinberg et al 1997).

COSMOLOGICAL PARAMETERS WITHOUT HYDRODYNAMICS Rerunning the simulations with different input parameters and/or evolving them over a long time span is expensive, as is the analysis of large observed and simulated datasets. A number of new semi-analytical techniques have been developed to avoid these difficulties. Although not "hydrodynamically correct" they can give new insights into important aspects of the sometimes obscure dependence of the observational properties on the underlying physical environment. Such techniques compensate for the absent hydrodynamics by various analytical recipes: Petitjean et al (1995), and Croft et al (1997b) used dark matter simulations and assume that baryons (furnished with a suitable analytical thermal history) trace the dark matter directly; Bi et al (1992), and Hui et al (1997) applied power spectra with various forms of cutoff to mimic the smoothing introduced by the Jeans length; Gnedin & Hui (1998), using a dark matter code, simulate the effects of the gas pressure by modifying the gravitational potential.

THE LYMAN ALPHA FOREST AS A RECORD OF PRIMORDIAL FLUCTUATIONS     Semianalytical work by Gnedin & Hui (1996) and Hui et al (1997) has elucidated the relation between column density peaks ("absorption lines") and the statistics of density peaks, and has given analytical expressions for the dependence of the shape of the column density distribution function f (N) on cosmological parameters. The slope of f (N) was found largely to be determined by the normalization and the slope of the initial mass power spectrum, with changes in the equation of state T = T() having an additional, but smaller impact. The overall normalization of f (N) is given by (_b h²)² / ; a change in this quantity shifts f (N) horizontally to larger N.

Croft et al (1997b) have suggested a technique for recovering the initial power spectrum of density fluctuations directly from the fluctuations of the optical depth. The distribution function of pixel fluxes in a Ly forest spectrum on larger scales is assumed to have originated via gravitational collapse from an initially Gaussian probability distribution of overdensities . Then the flux probability function can be mapped monotonically according to the rank of the flux values back onto a Gaussian probability function for the initial . The density power spectrum (width of the Gaussian) P(k) is then known up to a normalization, which can be derived from iterative cosmological simulations with the same P(k) but different normalization until the right flux power spectrum is obtained from simulated spectra. The flux power spectrum is unique up to a normalization which can be fixed by observing the mean absorption .

POTENTIAL PROBLEMS - UNSOLVED QUESTIONS     The new paradigm for the Ly forest has considerable explanatory power, but that does not mean that it is correct. The interpretation of the absorption systems, and the cosmological measurements planned or already performed to date depend on gravitational collapse as the dominant source of structure in the intergalactic medium. Even if the hierarchical models are basically correct, it is conceivable that local physical effects may upset some of the cosmological conclusions. A fluctuating radiation field may be a source of non-gravitational structure in the forest, as may be stellar feedback. How much of the absorption is caused by gas blown out by supernova explosions or stellar winds, and how robust are the cosmological conclusions in that case ? Metal enrichment has been found to be common for absorption systems with HI column densities as low as log N(HI) ~ 14 (Tytler et al 1995; Cowie et al 1995). If this is not due to a very early phase of metal enrichment we have to worry that some process other than gravitational collapse may have formed the metal enriched Ly clouds. The origin of the ionizing radiation and the spectral slope are another source of uncertainty. When and how do reionization and reheating happen, and where do the photons come from ? Is collisional reheating important, and how much do stars contribute to the UV flux, as a function of time ? On the technical side: Do hydrodynamic codes already converge, or how much do the inferred cosmological parameters (_b, the amount of small scale structure present) depend on the resolution and size of the simulations, and the numerical technique ?

Finally, the cosmological picture itself could be wrong, and the interpretation of the forest as absorption mostly by the intergalactic medium (as opposed to distinct galaxies) may be doubtful. Galaxy halos or disks could be big/numerous enough to produce the low column density Ly forest as well. For low redshift absorption lines, this last possibility has received much attention, and we will briefly consider this question next.