4. A MULTIDIMENSIONAL UNIVERSE

Cosmologies with extra geometric dimensions have been the center of much interest in recent years. A popular version involves ten dimensions, thus adding six new compact dimensions, over and above the familiar three-space and one-time dimensions. The radius of curvature of these extra-dimensions would be of the order of the Planck length (10^-33 cm), far smaller than the smallest dimensions within reach of presently operating accelerators (the TeV accelerator of Fermilab can probe to a few 10^-18 cm). Energies of the order of the Planck mass (10¹⁹ GeV) would be required to excite the corresponding modes. This is the reason why we can spend our life without being aware of the existence of these extra dimensions.

However they express themselves in others ways, well-known to us, but that we are just recognizing to be related to these extra-dimensions. Here I will discuss one of these manifestations which will bring us back to big-bang nucleosynthesis. In these cosmological models the values of the coupling constants of the various forces depend upon the radius of curvature of these compact dimensions. If, as is the case in our familiar 3-D geometry, these radii are changing with time, the coupling constants would also vary with time.

We have much evidence today that these coupling constants are faithful to their name. Again we can take advantage of the success of BBN to study the question. To what extent can we alter the value of these constants (through eq. (10) and fig. 1) without messing up the good agreement with the simple theory. The answer is the following: since the universe cooled off to less than one MeV, some ten billion years ago (after the first minutes in the standard chronology), the coupling constants have not changed by more than a few percent.

We are not used to question the constancy of the laws of nature. We usually take this fact for granted, or at least natural. The situation is changed when the extra-dimensions are added. Then the observed constancies serve as a severe constraint in the choice of the theories, just as the renormalizability of gauge theories has been a most useful guide in elementary physics research.

I will try to illustrate the situation by a simple case: the historical Kaluza-Klein model published in 1921. The aim of this model was to formulate an unified theory of gravitation and electromagnetism. One extra space dimension is added to the standard 3-D geometry. This space, with radius r too small to be detectable, is responsible for the electromagnetic force through which it manifests itself.

Assume a Fourier decomposition of a field in 5-D, where x represents the 4 familiar dimensions and y is the fifth one.

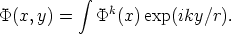
(14)

The five-D ⁵ Laplacian, applied to this field, will give the equivalent of a Klein-Gordon equation for massive particles:

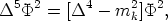
(15)

where m_k = k/r with k = 0, +1, +2 .....

If r is chosen as the Planck radius, the different modes correspond to particles with masses integers of the Planck mass, needless to say unobservable today. Our everyday physics involves only the k = 0 mode. It is to be derived from the 5-D action integral:

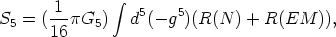
(16)

where G₅ is the fundamental Newton constant of the (real) 5-D world. The number 5 on the other letters of this expression are a reminder of the presence of the fifth dimension. R is the curvature tensor which includes both a gravitational (N) and an electromagnetic (EM) term related to Maxwell's equation.

By confining ourselves to the k = 0 mode of the field, it is clear from eq. (13) that the fields are no more functions of y. This dimension gets out of the dynamics. In consequence we may simply integrate eq. (15) over y, to obtain:

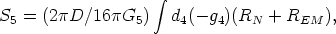
(17)

or

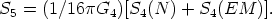
(18)

Thus we recover the standard 4-D physics if we identify the observed Newton's constant G₄ with G₅/D, where G₅ is the really fundamental constant of the theory. Hence the need to keep r constant to explain the observed constancy of G₄.

Since the years of the Kaluza-Klein theory, the gauge theories of weak and nuclear interaction have been developed successfully. The forces of nature are now seen as resulting from group symmetry operations in internal (isospin) spaces. The EM force correspond to an U(1) group, the full electro-weak force to an SU(2) × U(1) and the nuclear force to an SU(3). In analogy with the K-K model, the present view of multidimensional cosmologies is to identify the internal spaces of the standard gauge theories with geometric spatial dimensions on which the corresponding group operators would act. The motivation for this identification is related to the many difficulties of the standard models (divergencies, anomalies, etc.) together with the hope of formulating a realistic theory of quantum gravity. We know no other way to reach these goals.

The potential variability of the observable coupling constants of the various forces with the dimensions of the compact spaces is met in higher-D spaces just as in the 5-D space of K-K. In the Einstein cosmological versions of our expanding 3-D spatial universe, all the radii are coupled together so that variation of any one dimension always results in variation of the others. We know that our familiar 3 dimensions have expanded to some 10⁶⁰ times the Planck length in the last ten billon years. It is usually assumed that the other six dimensions have contracted upon themselves after a few Planck times (10^-43 sec). The situation is described in fig 4. The question in everyone's mind is: how did these dimensions managed to remain so amazingly stable while the others underwent such a large modification? It is fair to say that no satisfactory answer have yet (in 1987) be given to that question.

Figure 4. Cosmological evolution of space in a 10-D universe. Our familiar 3-D space is expanding with time, while the 6-D compact space rapidly reaches very small radii. The succss of big bang nucleosynthesis implies that these radii have not varied by more than a few percent since the first minutes. This constancy imposes severe constraints on superstring theories and, in general, on all extradimensional cosmologies.